Fatigue failure of materials and bonded interfaces is a complex topic and yet a quite important issue in engineering practice, since most structures are subjected to both applied and environmental cyclic loadings during their service life. The fatigue failure process has not been completely understood and there is no single accepted criterion or law to explain fatigue phenomena. However, the application of linear elastic fracture mechanics concepts has resulted in reasonable and useful explanations of fatigue failure, especially in crack propagation rate measurement and fatigue life prediction. It is generally accepted that there are three stages that characterize the fatigue process [17]: (I) near threshold region, (II) intermediate region, and (III) high growth rate region, as illustrated in Fig. 19.
The relationship between crack growth rate and fracture toughness was first established by Paris in the 1960s [18,19]. Paris introduced the well-known Power Law (or Paris Law) equation, which states that the crack growth rate da/dN, where a is the crack length and N is the number of cycles, depends mainly on the amplitude of the stress intensity factor AK:
where C and m are empirical constants dependent on materials, loading modes, environment and other factors, which need to be determined experimentally. Paris proposed an exponent m = 4 in agreement with his experimental data for metals. Subsequent researchers over decades showed that the exponent m in Eq. (2) was not necessarily equal to 4, and
|
Figure 19 Schematic illustration of the three stages of the fatigue process. |
the value varied depending on the type of material. It was found that the exponent m ranged from 2-5 for metals, was higher than 4 for many polymers and plastics and much higher for composite materials. The pertinent literature on application and development of various modified Paris Law formulations is reviewed by Jia et al. [7].
The load ratio R is believed to be an accepted significant parameter for fatigue crack growth rate. Many researchers have noticed that the original Power Law could not explain the load ratio effect, and therefore all kinds of modified Paris Law equations were proposed to include the load ratio effect. It is also well accepted that the threshold of the stress intensity factor range is changed with different load ratios. In this study, the load ratio effects on fatigue fracture of FRP-wood bonded interfaces using TDCB specimens [7] are summarized, and a modified Paris Law equation is proposed to characterize the crack propagation rate.
 15 июля, 2015
15 июля, 2015  Malyar
Malyar 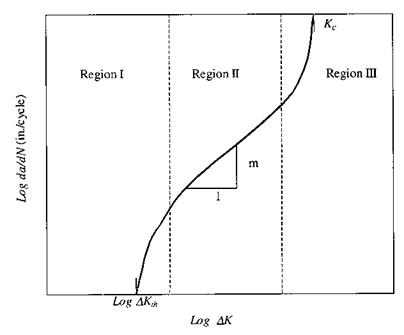
 Опубликовано в рубрике
Опубликовано в рубрике 