The branching coefficient as defined by Flory is a = the probability that a certain branched unit will be joined to a second branched unit rather than to a terminal group. For example, for a trifunctional monomer if a = 1/2 the molecule is a continuous chain equivalent in theory to a gel. In this case a = 1/2 is the critical condition defining the start of the formation of an infinite tridimensional network.
When the monomer has functionality greater than or equal to 3 the system will gel when a(f — 1) > 1. The critical value of a is then
where in Flory’s statistical gel theory a is = the functionality of the monomer of higher functionality when there are only two monomers taking part in the polycondensation reaction. So iff = 3 then a = 0.5. Iff = 4 then a = 0.33, etc. When a = 0 there is no reaction and when a > 1 the system never gels. The gel point of a thermosetting resin, hence of an
adhesive based on a thermosetting resin, depends on
1. the functionality of the monomers
2. the degree of conversion reached by the reaction
3. the ratio of the two monomers, or more exactly of the reactive sites/groups of the two monomers.
1. Case 1: Case of Reaction of a Trifunctional Monomer with a Bifunctional Monomer
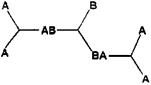
In the polycondensation of a trifunctional monomer with a bifunctional monomer
|
|
the limiting condition to gelling is then that a bifunctional B-B monomer must be linked to two branched monomers, hence bound to two trifunctional monomers. Thus, if the proportion of B-B is limited, the extent of branching is also limited. The limiting condition to start branching, hence for the start of gelling, depends on the probability that segments -AB-BA — do indeed exist. In the theory all groups are considered as they cannot react with groups of the same kind (thus A can only react with B) and all groups have the same reactivity: the probability that the first group A (the one on the left) has then reacted with a group B is pA, namely the fraction of all the groups A which have reacted. The probability that the second group B (the one on the right) has reacted with a group A is then pB. The probability then that the segment — AB-BA — occurs is
pa pb therefore
a = pa pb (2)
which is the probability of a joint between two branching sites. As the functionality of the monomer of higher functionality in this example has been taken as f = 3 then a = 0.5. this means that at the gel point
(pA pB)gel = a (3)
As the initial concentrations of reactive groups A and B are considered here to be the same, then pA = pB = p and hence
pjJel = a and pgel = a1/2 (4)
Which gives
pgel = 0.707 (5)
Where pgel is the degree of conversion at the gel point which means that 70.7% of the reactive groups/sites of the system have reacted at the gel point.
2.
 |
Case 2: Case of Two Trifunctional Monomers The polycondensation of two trifunctional monomers
In this case it is necessary that an — AB — joined segment exists between branching sites. This is equivalent to saying that
a = pA or pB (depending which one is less) (6)
when A and B are at the same initial concentration. Thus, pA = pB = p, and the limiting condition for a gel to form will be
a = p (7)
![]() 0.5, the limiting condition for a gel to form will then be
0.5, the limiting condition for a gel to form will then be
![]() pgel — 0,5
pgel — 0,5
Where pgel is the degree of conversion at the gel point which means that 50% of all the reactive groups/sites of the system have reacted at the gel point.
These two cases are valid also for monomers of higher functionality with the provision that higher functionality means a different value of f, hence a different value of a. Thus, in the case of polycondensations based only on two monomers there are only two possible cases to consider, one in which a bifunctional monomer is also present, and the other in which only monomers of functionality greater than or equal to 3 are present in the reaction medium. To take into account the cases in which the reactive sites of the two molecules are not equimolar one can define a ratio r as the ratio of the number of reactive sites A and B, with the proviso that r must always be smaller than or equal to 1 (so, if A>B r = B/A and vice versa if A < B r = A/B; If r is greater than 1, absurd results are obtained and the theory cannot be used) [15]. The simpler form of the equations defined by Flory to describe the two cases above are then
and
pgel = “ (9)
These equations are in their simplest usable form. The original equations of Flory took into account also the density of the hardened polymer. It has been disregarded here as it is of no consequence in the formulation of thermosetting adhesives discussed later.
3. Case 3: Case of Many Mono-, Bi-, Tri-, and Multifunctional Monomers The equations described in the previous two cases are not applicable to polycondensation systems in which either monofunctional monomers are present or a great number of branching monomers of a number of different functionalities of both type A and B are present. If one considers the most general case of a polycondensation system as
A + A2 + A3 H—— + Ai + B + B2 + B3 H——- Bj! polymer network
in which are present: (1) monomers the functionality of which is between 1 and i for the reactive groups A, and (2) monomers the functionality of which is between 1 and j for the reactive groups B, the degree of conversion and advancement of the polycondensation reaction at the gel point is given by the following equation [15-17]:
/’g’l = [r(fA — 1)C/b — 1)]1’2 <10)
where fA and fB are the weighted average functionalities of the reactive molecules A and B respectively, and where r is the same as above and represents the difference in stochio — metric proportions of the reactive sites. fA and fB are defined as
where NAi are the number of moles of Ai containing fAi functional groups for each A-type molecule. The use of these equations is better shown by an example. Thus, for the following complex system of reagents
4mol A 2 mol B
51 mol A2 50 mol B2
2mol A3 3mol B3
3mol A4 3mol B5
![]() Ш±25і)+32) + 4(3) =
Ш±25і)+32) + 4(3) =
|
[12 (4) + 22(51) + 32(2) + 42(3)] |
|
[12 (2)- |
|
22(50) |
|
32(3) |
|
52(3)] |
1(2) +2(50) +3(3) +5(3) ‘
This indicates that in such a complex polycondensation system gelling occurs when 77.11% of the reagents have in fact reacted. Equation (10) is then particularly useful when using Flory’s statistical theory of gelation. Owing to its simplicity and ease of use, Flory’s theory of gelation is the most useful theory to use for the formulation of thermosetting polycondensation adhesives. Flory’s theory presents, however, a problem: it underestimates the degree of conversion at the gel point by around 10%. This means that an experimental value of pgel = 0.770 corresponds to a calculated value of pgel(Flory) = 0.700-0.710. This is due to not being able to take into consideration cycli — zation reactions, a fact established by Stockmayer, so this theory is often known today as the Flory-Stockmayer gelation theory.
![]()
![]() Other theories, however, do exist, but the majority of these were published well after Flory’s. These theories became increasingly complex and notwithstanding that they allowed perhaps a somewhat better precision in the determination of pgel, the equations derived from them are so complex that in practice they are never used. This unnecessary complexity trend has gotten out of hand in certain cases to the level of a purely mathematical exercise rather removed from reality [12-14].
Other theories, however, do exist, but the majority of these were published well after Flory’s. These theories became increasingly complex and notwithstanding that they allowed perhaps a somewhat better precision in the determination of pgel, the equations derived from them are so complex that in practice they are never used. This unnecessary complexity trend has gotten out of hand in certain cases to the level of a purely mathematical exercise rather removed from reality [12-14].
However, a second theory, older than Flory’s, does indeed exist. This is the theory of Carothers. According to Carothers
DP„ — —^ (12)
2 — fP
where DPn is the number-average degree of polymerization and f is the average functionality of the system (a concept different from that of Flory’s) which is equal to
[Na fA + NBfB] [Na + Nb]
where Na and Nb are the numbers of moles of monomers A and B, and fA and fB are the functionalities, respectively, of monomers A and B. The degree of conversion in this theory is defined by the equation of Carothers
Because DPn becomes very large at the gel point as p tends to 2/f, the critical condition for gelling is defined in the Carothers equation as
![]() pgel —
pgel —
While the theory of Flory underestimates the gel point, the theory of Carothers overestimates it. For example, for the case of a trifunctional and bifunctional reaction system presented above, at equimolar reactive groups, while Flory’s theory forecasts pgel — 0.707, Carothers theory forecasts a value of pgel — 0.833, while the experimental pgel is 0.765-0.775. Recently, however [18,19], thermodynamic reasons why the two formulas should be combined came to light. This led to the proposal of a very simple equation affording much higher precision than each theory alone. This simple equation also gave much better precision of all the very complex and difficult to use theories devised and presented since Flory’s 1942 one:
p (2/f ) + (a/r)1/2
pgel — л
or
This equation is nothing other than the average of the equations of Carothers and Flory, and for instance yields a pgel — 0.770, while the most exact of the complex theories yields a pgel — 0.800 [18,19] for the simple case just shown above. The 1/2 operator is not there (but a/r is) in the case where no bifunctional monomer is present. This is valid also for the generalized Eqs. (17) and (18) which follow and which have been developed from Eq. (16) above. For two monomers, Eq. (16) can be developed to eliminate the presence in the
equation of two different ways of expressing functionality [Carothers’ average functionality of the system in the same equation in which appears (hiding in a) Flory’s functionality]. Equation (16) can then be expressed in the same functionality, so as to eliminate such a discrepancy.
![]() _ nA + ив 1 / /вив 1/2
_ nA + ив 1 / /вив 1/2
^Sd fAnA + fBnB 2 Za«a(/a _ 1)
In the case of a system of more than two monomers where each monomer can react with the other but not with itself the general formula becomes
In the most common case in thermosetting polycondensation adhesives, namely a reaction system composed of three monomers in which two can both react with the third one but where the former two cannot react with each other (and no monomer can react with itself), the equation for higher precision determination of the degree of conversion at the gel point becomes
It is easy to see from these equations that these higher precision equations become rapidly more difficult to use and to handle as the polycondensation system becomes more complex. Thus, Eq. (16) for two-reagent systems is used very easily, and Eq. (19) for three — reagent systems is still relatively easy to use, but for more complex systems Eq. (10) [15-17] is easier to use notwithstanding the 10% lower value it gives.
 29 июня, 2015
29 июня, 2015  Malyar
Malyar 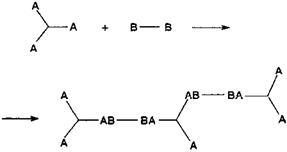
 Опубликовано в рубрике
Опубликовано в рубрике 