The molecular mechanics approach just described functions well, but the manner in which it has been used in the previous section is rather limited to static situations: dynamic situations can also be described well, although by a series of finite steps of ‘‘before and after’’ static calculations to ascertain the changes which have occurred or while they are occurring. Even the most modern molecular mechanics and dynamics programs still work in this manner. It might appear otherwise to a user, but every automatic molecular mechanics or dynamics computational program still works by a sum of small static situation steps, even if infinitesimally small. There is nothing wrong in such an approach of course, as it has been proven to work rather well even in the most complex situations. However, it is interesting to examine how such an approach works for systems in which movement at the molecular rather than atomic level is inherent in the definition of the system itself.
As regards adhesives proper only two series of studies fall in this category [9,71]. The first one of these models the process of chromatography [9]. There is no doubt that chromatography is a clear case of differential, competitive sorption, and hence a case of differential, competitive adhesion. Movement is inherent in the definition of the system, and predominance of secondary force interfacial interactions is inherent to the system too.
The study [9] concerns the achiral paper chromatography separation of three dihy — droxydiphenylmethanes (the three PF resin adhesive dimers discussed earlier in this chapter) on crystalline cellulose, and checks whether the results, the relative Rf values obtained by experimental chromatography, correspond to the interaction energies calculated at the interface. The algorithms used were the same as used for the previous approach. The results obtained were excellent, showing not just a trend correspondence between experimental Rf values and calculated energy values but even very close numerical correspondence with the actual relative values of Rf for the three compounds. One of the most interesting findings was that in the case of the interaction with a substrate of a homologous series of chemical compounds, the solvent or mixture of solvents could be easily modeled by just varying the dielectric constant used in the model. Such a result is of importance because it spares in many ternary systems the need to model the third component of the system, namely the solvent or the water present either in the polymer or in the substrate (such as in wood and cellulose).
The work was continued on the paper chromatography modeling of UF oligomers [72]. In this series of experiments the limits of the molecular mechanics approach finally started to become apparent. While a good trend correspondence with experimental Rf values was again obtained within each of the two series of UF oligomers tested, correspondence was lost when one tried to compare the compounds within a series with the compounds of the other series. Thus, excellent correspondence existed within the homologous series urea, methylene-bis-urea and dimethylene-triurea, and within the second homologous series monomethylol urea, N, N0-dimethylol urea, trimethylol urea, mono — methylol methylene-bis-urea, and N, N0-dimethylol methylene-bis-urea, but not between the two series. It became evident that to compare within two nonhomologous series of compounds it would be necessary to model the water in the system as a third group. Thus, the conclusion was that the wise use of the dielectric constant to spare modeling a ternary system was very valid, but only when the molecules to be compared belonged to a homologous series of compounds; If they were not, one needed to model the solvent too as a separate species [72]. There is no doubt that this can be achieved, either by a classical molecular mechanics method, or even better by modeling the solvent through a molecular dynamics approach in which a solvent layer is modeled as in Section III for the generalized system while the substrate and the polymer are still modeled by more classical molecular mechanics approaches. The study of the chromatography of UF adhesives on cellulose did not have such an industrial importance to warrant such an extensive, further investigation. Thus, the next investigation centered instead on the more difficult ternary systems but for a totally different set of molecules: this is the work on varnish/primer/cellulose systems reported earlier in this chapter.
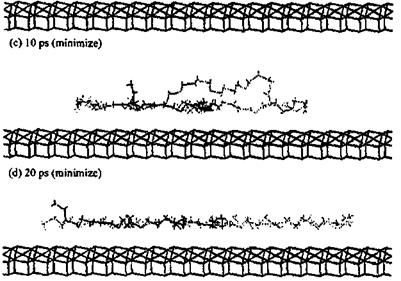
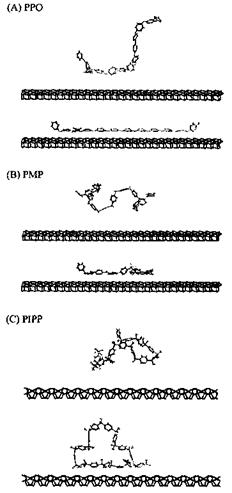
The second study [71] is even more interesting and concerns the simulation of different polymers adsorbed onto an alumina surface. The alumina surface was modelled and a number of different polymers were modeled at the polymer-alumina interface. Among the adhesives modeled on the surface of alumina were polyolefins, several polyacrylates, polyoxides, polyols, and the polyphenyl bridges in epoxy resins, in diaminodi — phenylsulfones and in diaminodiphenylmethanes (the same PF dimers modeled above on the surface of cellulose). The authors found that the method not only facilitated visualization of the preferred orientation of the adhesive chains with respect to the substrate surface (Figs. 7 and 8), but also indicated which groups were critical in determining such orientations. Their results again confirmed what was found in all previous studies that even in such a different series of adhesive/substrate systems the polymer structure which deformed easily was favorable to a more optimal orientation for adsorption on the substrate surface. The authors could identify which — CH2- groups and phenylenes in the backbone of the polymer were conductive to such deformations, and that the alkyl side groups found it more difficult to yield optimal deformation during the adsorption process, but were still able to produce strong adhesion once they had been adsorbed. Besides, the polyphenyl linkages revealed a wide low energy region in the rotations of torsional angles, this being favorable to deformation of the polymer chains with pheny- lene linkages in the backbone leading to large adsorption energies. Polar side groups instead were found to increase adsorption, confirming previous results, and in line with expectation. While the range of energy results reported was quite limited, as one could understand by the number of different cases approached, the study can be considered more as a purely comparative scan of the behavior of certain adhesives on an alumina surface rather than an in-depth investigation of the behavior of each adhesive/substrate system. Notwithstanding this, the calculated results once again could be qualitatively correlated with experimental observation, and the order of the energy interactions was shown to be the same. These results showed again how simulations by molecular mechanics/dynamics could potentially by used to facilitate the design of improved adhesives.
|
|
|
Figure 7 Simulation of the adsorption of poly(tetrahydrofuran) (PTHF) on an alumina surface for 20 ps. (From Ref. 71.) |
The material discussed in this chapter should give the reader a brief overview of what has already been achieved in the field of molecular mechanics to improve adhesion or to explain adhesion phenomena. More will surely be achieved in times to come by the application of such tools to adhesion problems. Molecular mechanics and dynamics then present a powerful tool which should not be ignored in the field of adhesion and adhesives.
|
|
Figure 8 Simulated adsorption by molecular dynamics of (A) poly (p-phenylene) oxide (PRO), (B) poly(methyl-1,4-phenylene) (PMP) and (C) poly(iso-propyl-1,4-phenylene) (PIPP) on an alumina surface showing substantial structural changes during the adsorption process (upper figure: initial conformation; lower figure: = adsorbed conformation) (From Ref. 71.) Note the formation or absence of adsorption loops in the polymer chains for the different cases.
 29 июня, 2015
29 июня, 2015  Malyar
Malyar 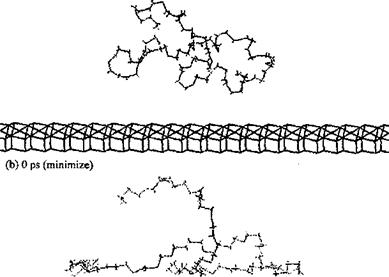
 Опубликовано в рубрике
Опубликовано в рубрике 