Лако-красочные материалы — производство

The mechanics of particle adhesion and the deformations resulting from the stresses generated by adhesion forces have now been studied both experimentally and theoretically
for a long time. Most of the approaches taken on the subject stem from a thermodynamic rather than a molecular viewpoint, such as the use of the so-called Johnson-Kendall — Roberts (JKR) model [14]. The first time that such a type of problem was approached from a molecular viewpoint was the proposal by Derjaguin et al. of a new adhesion model (the Derjaguin-Muller-Toporov (DMT) model) [15]. Soon afterwards, the Muller — Yushchenko-Derjaguin (MYD) model was proposed by Muller et al. [16,17] by assuming that the adhesion forces, and hence the interaction between a particle and a substrate could be represented by Lennard-Jones potential functions. With this theory it is not possible as yet to speak of a molecular mechanics approach. Nonetheless, this is the first educated assumption and understanding that the interaction of generalized particles, atoms, and molecules can be described even for problems and theories of adhesion through Lennard-Jones functions, one of the classical type of potential functions used to describe interactions in molecular mechanics. This insight perhaps opened the way to the subsequent use of molecular mechanics in the field of adhesion. The JKR and DMT models have since been shown to be particular subsets of the more general MYD theory. They have been extensively studied [18-21] and models have been presented.

While all these theories have helped our understanding of particle adhesion, all of them suffer from the considerable drawback of treating the mechanical response of mate­rials as something totally independent of the molecular level parameters influencing adhe­sion. As the intermolecular potential of a material determines, or at least strongly influences, both its mechanical properties as well as its surface energy the possibility exists that a more holistic adhesion model could be conceived by going back to the drawing board and starting from first principles. This, added to the fact that the theories briefly referred to above do not always predict the correct value of the power law depen­dence of the contact radius on particle radius prompted some attempts in this direction. Notable in this respect are two investigations, and only here for the first time in this chapter one can really speak of a molecular mechanics approach to some form of adhe­sion. The first investigation [22] was based on molecular mechanics calculations of the interaction of acrylic-type monomers with an idealized model surface composed of a rectangular parallelepiped of generalized, idealized atoms treated as spheres arranged at regular nodes of a square grid network and constitutes the first example ever of this type of approach. The second one followed four years later and went further [23-25]. It was a molecular dynamics study along very similar lines as the previous one, defining the interaction between the two surfaces of generalized, idealized atoms treated as spheres. It is this latter study which will be briefly presented and discussed, with all its advantages and limitations, because it is a more clear-cut case of a generalized model of particle adhesion based on molecular mechanics. The former and earlier model will not be dis­cussed further as it really constitutes a hybrid case between the type of approach presented in the following section of this chapter dealing with examples of even earlier but concep­tually more correct nongeneralized models, and the type of approach based on particle adhesion proper.

Before getting more involved in the finer points of particle adhesion studies by molecular mechanics it must be pointed out that such an approach suffers from consider­able drawbacks. Molecular mechanics and dynamics by definition involve interactions between clearly defined types of atoms, with clearly defined atomic characteristics, placed in clearly defined molecular structures. Thus, a generalized, fictitious surface of only, let’s say nitrogens, or even worse of generalized spheres, is a rather extreme physical approximation. It is by definition incorrect in a molecular mechanics and dynamics inves­tigation. Such a drawback needs to be pointed out to put in perspective and understand
the limitations inherent in a model pretending to describe atomic and molecular interac­tions in real systems by a molecular mechanics approach oversimplified at the physical level. Nonetheless, valuable information has been gathered by this type of approach. It is furthermore a very good approach for the description of particle/particle interactions when the particles themselves are composed of well-defined atom types interacting with each other both at the particle/particle interface and within the body of the particle itself.

The more advanced work today on particle adhesion [23-25] builds then on the assumption that particles interact through a Lennard-Jones-type potential function, namely

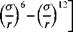(6)

where є is the binding energy between an atom and its nearest neighbor and a is the distance between the two atoms when the value of the potential energy represented by the above function is neither attractive nor repulsive: namely at the crossover intersection point of the function with the axis. The authors of the theory recognized that the choice of this potential was purely empirical [25].

At first a flat surface of atoms was generated in a stepwise manner allowing the energetics associated with the creation of the surface to be determined, and then two of these surfaces were brought together and allowed to form a bond. The pairs of mated surfaces were then separated in a constrained tension test to form two fracture surfaces. The potential energy of the system and the axial stresses used to produce the displacements observed were monitored. The molecular mechanics computational modeling part con­sisted in assembling a parallelepiped of generalized atoms as spheres, arranged in a pre­determined regular array. The computational model used in tension, compression, and shear modes allows examination of the stresses produced when free surfaces approach one another. The parallelepiped of atoms constituting each surface was composed of 768 atoms aligned parallel to the X, Y, and Z axes of a reference system. The parallelepiped of atoms was then constituted of 24, 8, and 8 layers of atoms in the X, Y, and Z directions, respectively. By the time the first 100 iterations were terminated the system temperature had fallen to half of its original value as a consequence of the equipartitioning of the energy into kinetic and potential contributions. The lateral dimensions of the surface that was about to be created were then fixed by putting back the atoms in their previous positions after each computation inducing, as a consequence, a gradual increase of the gaps between atoms without actual movement of the atoms. This effectively suppressed the usual atomic motions allowing the variation of the apparent potential energy of the system as the surfaces were separated be followed computationally. Once the size of the interatom gaps had increased to the size of the cut-off radius there was no further increase in potential energy with increasing gap size. Once the gap was established the atomic motions and temperature dependence were reactivated to allow the system to relax into its new state of equilibrium.

Once the free surfaces in equilibrium were computationally generated they were brought closer to one another by a very slow approach rate of 10,000 iterations to reduce the gap between the surfaces to one cut-off radius. The slow approach was neces­sary to minimize or eliminate complications arising from spheres’ (atoms’) impact ener­gies. All this allowed changes in potential energy and the following of the resulting surface interactions which developed at constant temperature and constant dimensions. During the approach the mutual attraction increased monotonically until a certain critical stress level was reached. At such a critical stress the two surfaces lept into mutual contact as the
strain energy increased because the rate of energy storage due to elastic deformation equated to the rate at which energy was provided by the attraction between the surfaces. Thus the model was able to reproduce, at least qualitatively, the leap-to-contact effect between a particle and a planar surface observed experimentally using atomic forces techniques [26-28]. In the cases where the surfaces were pulled, rather than lept, into contact the stresses were not uniform and traveling waves were generated. Additional traveling waves were also generated when the surfaces struck one another. These waves, which interacted with each other, correspond to atomic level kinetic energy and can be interpreted as an increase in temperature. As a consequence, the authors came to the interesting conclusion that in a real system this implied that energy loss occurred even if only elastic deformations resulting from the forces of adhesion were considered: hence, not all the energy is recoverable on surface separation as not all the energy of the system is stored elastically.

Study of the model during subsequent separation of the two surfaces, this corre­sponding to a tension, showed clearly the existence of hysteresis effects. This hysteresis might account for the effect of Young’s modulus on particle adhesion, which is not pre­dicted in the JKR model. In the simulation of the process of separation of the two surfaces and of the fracture mechanics of the model, fracture finally occurred only when the interatomic spacing of some regions exceeded the critical value to an extent that further separation reduced suddenly the energy. This occurred suddenly and over a very small number of iterations. Even in the case of surface separation, waves were generated which decayed as a function of time thus generating thermal energy which was then lost by the modeled system. Thus, even during elastic deformation, surface separation energy loss mechanisms exist. The maximum stress experienced in the leap-to-contact decreased with increasing temperature while the average stress, shortly after leap-to-contact, was much less sensitive to the temperature. Finally there was a distinct offset between the initial and final potential energies due to microstructural changes in the interfacial regions as the two layers of atoms near each of the two surfaces contained numerous site defects, namely atom sites which were empty.