The mean field theory allows the calculation of many physical properties of adsorbed polymer layers. For most experimental situations it gives a good qualitative description, but it is known not to be quantitative as it implicitly ignores the concentration fluctuations associated with the excluded volume interaction. A simple strategy is to assume that the mean field theory gives the correct picture and to take the concentration fluctuations into account using a scaling approach. The first scaling description of adsorbed polymer layers is due to de Gennes [26]. The starting point is to assume that the local structure of an adsorbed polymer layer is similar to that of a semidilute solution and can be described as a fluctuating network with a local mesh size £(z). In a good solvent, the local correlation
|
Figure 6 Self-similar concentration profile: at a distance z from the surface, the local mesh size of the temporary polymer network is proportional to z. |
length varies as §(z) ~ [c(z)]_3/4. At intermediate length scales between the adsorption length b and the polymer radius R the only relevant length scale is the distance to the surface z. The local mesh size must, therefore, be proportional to the distance z. This leads to a power law decay of the monomer concentration c(z) ~ z_4/3 and to a concentration profile that is self-similar as represented in Fig. 6. The minimum size of the loops is the adsorption length b and the maximum size the chain radius R. Note that if the mean field expression for the correlation length is used § ~ c_1/2, and the scaling argument is consistent with the mean field theory (c(z) ~ z“2). The scaling approach is not refined enough at this level to distinguish between monomers belonging to loops or tails. It can, however, be improved in order to incorporate the differences between loops and tails [27]. As in the mean field theory, loops dominate close to the surface and tails dominate in the outer part of the layer. The crossover distance between these two regions is 1 ~ N1/2. The probability of having a loop of g monomers is found to be p((g) ~ g_(1+2v) where v = 3/5 is the swelling exponent; the probability of having tail of g monomers is pt ~ g(y ~v)/2 “1 where the exponent у is roughly equal to 1.16. Note that the average loop length is very small (of order 1) and that the average tail length is very large (of order N). This scaling approach gives an accurate description of the structure of adsorbed polymer layers as probed, for example, by neutron scattering [28].
 27 июня, 2015
27 июня, 2015  Malyar
Malyar 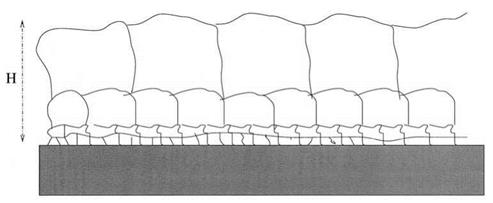
 Опубликовано в рубрике
Опубликовано в рубрике 