В предыдущем разделе при рассмотрении структурно-механических особенностей коллоидных систем мы считали эти системы жидкостями. Однако ряд свойств коллоидных систем можно объяснить, если рассматривать их как твердые тела. Последний подход особенно целесообразен при изучении коллоидных систем, обладающих в некоторой степени упругостью или эластичностью и характеризующихся наличием истинного предела текучести (предела упругости), т. е. такого предела напряжения сдвига, ниже которого практически никакого течения не наблюдается Как правило, таким свойствам отвечают достаточно концентрированные твердообразные гели и системы с конденсационно-кристалли — зационной структурой
Однако прежде чем рассматривать механические свойства упругих гелей, «становимся кратко на таких важных для понимания этих свойств характеристиках систем, как модуль сдвига и период релаксации напряжения.
Модуль сдвига Е, как известно, характеризует жесткость всякого тела м его способность сохранять форму. Эту величину можно вычислить из известного уравнения Гука: /
Е*=Р/Е (Х, П)
Тде е — относительная деформация сдвига в истинно твердых телах; Р — напряжение сдвига.
Это уравнение справедливо лишь при малых деформациях, так как при определенном критическом напряжении, называемом пределом упругости, тело теряет упругие свойства и сохраняет остаточные деформации. Модуль сдвига Е •при одинаковой скорости приложения нагрузки зависит от природы тела и температуры Для твердых тел величина Е может достигать весьма больших значений, для истинных жидкостей Е — 0, так как всякое сколь угодно малое напряжение сдвига приводит к течению жидкости. Ниже в качестве примера приведены значения модуля сдвига Е (в кгс/смг) для некоторых веществ:
Желатин
0,5%-ный раствор…………………………… 4 • 10—
TOC o "1-3" h z 10%-ный раствор (студень) . . 5*10-
Каучук………………………………………………………. 1,7 • 10»
Свннец………………………………………………. 4,8-10*
Дерево (дуб)……………………………………….. 8-Ю4
Сталь………………………………………………… 8-Ю5
А. А. Трапезников показал, что весьма характерным реологическим параметром системы является предельная обратимая деформация сдвига вмакс, достигаемая в быстро релаксирующих системах (о релаксации см. ниже) при высокой скорости деформации. В различных коллоидных системах она может быть весьма разной. Например, в пастах она обычно составляет несколько процентов или десятков процентов, тогда как в эластичных гелях и некоторых растворах полимеров она может достигать десятка тысяч процентов. Такие значення намного превышают привычные значения предельных обратимых деформаций сдвига каучуков.
Период (или время) релаксации связан с тем, что обычно молекулы или другие структурные элементы материальной системы обладают некоторой подвижностью и способны перемещаться относительно друг друга. В результате этого напряжение, создавшееся в теле вследствие его деформации, способно со временем в значительной степени «рассасываться». Подобный процесс уменьшения напряжения во времени получил название релаксации. Релаксация является следствием теплового движения и имеет совершенно общий характер.
Предложен ряд уравнений, описывающих деформацию систем, способных релаксировать Наиболее простым является уравнение Максвелла, вытекающее из его теории упруго-вязкого тела:
DP/dr = Е (de/dx) — (Р/т*) (X, 12>
Где х*— константа, называемая периодом или временем релаксации.
Легко убедиться, что уравнение Максвелла передает качественно основные закономерности релаксации при постоянной температуре. Еслн деформацию тела поддерживать постоянной (е = const), то De/Dx •= 0 и из уравнения Максвелла следует, что напряжение Р меняется со временем по закону:
(dP/dx) + (P/Тг*)=0 (X, 13)
Проинтегрировав это уравнение, получим
Р = Р0е~х’х* (X, 14)
Отсюда видно, что с течением времени напряжение в деформированном теле убывает по экспоненциальному закону, а константа х*, характеризующая скорость релаксации, равна промежутку времени, в течение которого начальное напряжение тела при постоянной деформации уменьшается в е ш* 2,72 раза (е — Основание натуральных логарифмов).
Периоды релаксации напряжения низковязких жидкостей весьма малы вследствие большой подвижности их молекул. С увеличением вязкости периоды релаксации жидкостей возрастают и приближаются к периодам релаксации напряжения твердых тел. Для кристаллов процесс релаксации протекает бесконечно медленно. Ннже в качестве примера приведены значения периода релаксации напряжения т* (в с) некоторых веществ:
Вода………………………………………………………………… 3’1°і!!
Масло касторовое……………………………………………………. 2*10
Лак копаловый……………………………………………………. 2-Ю
Каннфоль (при 55 °С)…………………………………………….. 5’10
Желатин, 0,5%-ный раствор……………………………………. 8* 102
Канифоль (прн 12 °С)…………………………………………… 4-10°
Идеально твердые тела………………………………………………… оо
Обращает внимание сравнительно большой период релаксации для весьма разбавленного 0,5%-ного водного раствора желатина Период релаксации для этого раствора ближе к периоду релаксации напряжения твердых тел, чем к периоду релаксации напряжения жидкостей. Это объясняется наличием в растворе желатина сравнительно больших структурных элементов (макромолекул желатина), требующих для перегруппировки сравнительно большого времени.
Часто при деформации реальных тел наряду с явлениями релаксации наблюдается так называемая запаздывающая упругость. В то время как релаксация приводит к переходу упругой деформации в пластическую, запаздывающая упругость проявляется в том, что не вся упругая деформация возникает мгновенно (как в идеально твердых телах). Часть этой деформации развивается во времени, так что упругая деформация достигает предельного значения, отвечающего заданному напряжению, лишь после определенного промежутка времени. Как правило, запаздывающая упругость проявляется тем сильнее, чем неоднороднее структура твердого тела.
Возвратимся к рассмотрению механических свойств твердообразных микрогетерогенных и коллоидных систем, обладающих истинной упругостью. К таким системам относятся поликристаллические металлы, самые разнообразные структурированные дисперсные системы, гели, концентрированные растворы мыл, а также высокомолекулярные вещества н их концентрированные растворы, способные проявлять не только упругость, но н высокую эластичность.
Поведение всех этих систем при незначительных деформациях сходно с поведением идеально упруги^ тел. Однако при напряжениях, ведущих к разрушению структурной сетки, эти системы способны течь как вязкие жидкости, причем их эффективная вязкость всегда падает с увеличением скорости течения или напряжения.
Очень часто при деформации этих систем явления упругой (мгновенной) деформации, запаздывающей упругости и течения накладываются друг на друга и дают характерную картину изменения суммарной деформации во времени, представленную на рис. X, 8 Как можно видеть, под влиянием деформирующей силы, например напряжения сдвига Р, приложенного к системе в момент Ті, развивается мгновенная упругая деформация еь Этой деформации отвечает мгновенный модуль сдвига Е — Р/е.. Затем система под действием силы начинает течь в результате необратимой перегруппировки структурных элементов. Одновременно в системе развивается запаздывающая упругость, обусловливающая деформацию &2 вследствие обратимой перегруппировки структурных элементов Этой замедленно развивающейся упругой деформации отвечает модуль сдвига Ег — Р/е2. Все это приведет к тому, что кривая на рис. X, 8 будет асимптотически приближаться к некоторой прямой, — соответствующей течению системы. Если через некоторое время в момент деформирующее усилие будет устранено, упругая деформация Єї исчезнет со скоростью звука. Далее постепенно исчезнет деформация е2, обусловленная запаздывающей упругостью, а деформация 83, обусловленная течением (истинной релаксацией), осгаиется как необратимая.
|
|
|
Рис. X, 8. Зависимость деформации в от времени т при постоянном напряжении для системы, обнаруживающей мгновенную упругость, запаздывающую упругость и течение. |
Иногда найденная в этих условиях необратимая деформация представляет собой не истинно пластическую, а кажущуюся пластическую деформацию, являющуюся следствием того, что процесс восстановления формы деформированного тела происходит чрезвычайно медленно. В последнем случае остаточная деформация частично или полностью исчезает в результате определенной обработки тела (например, нагревания или набухания в растворителе), обусловливающей более быстрое протекание перегруппировки структурных элементов. Это указывает на то, что деформированное тело после снятия прило
женной извне нагрузки может иметь скрытую упругость. Упругость, т. е. способность дисперсной системы после прекращения действия деформирующей силы возвращаться к первоначальной форме, как правило, указывает на особую внутреннюю структуру системы, препятствующую необратимому смещению ее элементов по отношению друг к другу.
Определение механических свойств коллоидных систем
Жесткие системы, обладающие достаточной механической прочностью, можно исследовать обычными методами физико-механического анализа (снятие кривой, характеризующей зависимость от деформации напряжения, определение предельного напряжения прн растяжении или сдвиге, определение относительной.
|
|
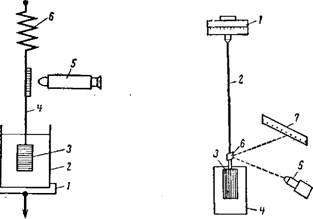
Риг. X, 9. Схема прибора Вейлера и Рис. X, 10. Схема крутильного при-
Ребиндера для определения струк — бора для определения структурно-
Турно-механических свойств дисперс — механических свойств дисперсных
Ных систем: систем:
1 — столик; 2 —кювета; 3 — рифленая пла — / — крутильная головка; 2 —упругая нить;
Стинка; 4— жесткая нить; 5 —микроскоп; 3 —рифленый цилиндр; 4 — кювета; 5 —осве — 6 — динамометр. титель; 6—зеркальце; 7 — шкала.
И остаточной деформации и т. д.). При этом необходимо лишь учитывать скорость деформирования, так как последняя сильно влияет на полученные результаты.
Для определения механических свойств гелей и других структурированных дисперсных систем, обнаруживающих упругость, предложен ряд специальных методов, из которых рассмотрим здесь только два.
Метод тангенциального смещения пластинки. Принцип этого метода, предложенного С. Я. Вейлером и П. А. Ребиндером, заключается в определении усилия, необходимого для смещения пластинки, погруженной в исследуемую систему. Устройство прибора, с помощью которого осуществляется измерение, схематически показано на рис. X, 9.
Прямоугольная рифленая пластинка 3 подвешена с помощью жесткой нити 4 К пружинному динамометру 6. Пластинку полностью погружают в исследуемую дисперсную систему, помещенную в кювету 2 до начала испытания. Кювету с дисперсной системой закрепляют на подъемном столике 1. При’ опускании с постоянной скоростью столика с кюветой пружина растягивается и в системе возникает напряжение сдвига, которое, очевидно, пропорционально растяжению пружины. Последнее может быть измерено с помощью микроскопа 5, снабженного окулярным микрометром, или с помощью микрошкалы.
Напряжение сдвига Р вычисляют по растяжению предварительно прокалиброванной пружины и соответствующему этому растяжению усилию F по урав-
Р-/7(2«> (X. 15»
Где S — боковая поверхность пластинки 3.
Предельное напряжение сдвига 0, характеризующее прочность структуры сиетемы и соответствующее наибольшему усилию (при отсутствии скольжения системы вдоль поверхности пластинки), вычисляют по уравнению.
Е —*W/(2e) (X, 16)
С помощью описанного прибора можно определять ие только предельное напряжение сдвига, но и модуль упругости, эффективную вязкость, исследовать процесс релаксации, а также снимать полные деформационные кривые е, Р при разных скоростях деформации.
Метод закручивания цнлнндра. Впервые метод определения упруго-пластических свойств структурированных систем по закручиванию цилиндра, подвешенного на упругой нити и погруженного н исследуемую систему, был, как мы уже указывали, предложен еще Ф. Н. Шведовым н 1889 г. На рис. X, 10 приведена схема прибора, с помощью которого выполняется определение. Прибор имеет крутильную головку 1, в которой закреплена упругая нить 2. На нити поднешеи рифленый цилиндр 3 с ‘зеркальцем 6. Цилиндр 3 полиостью погружают в кювету 4 с исследуемой сцстемой. При повороте крутильной головки на определенный угол а крутящий момент передается через нить цилиндру и вызывает сдвиговые деформации в слое системы, окружающем цилиндр. Цилиндр также поворачивается иа некоторый угол (J до равновесия между упругим напряжением нити и сопротивлением деформируемой системы. Разность (ос — Р) дает угол закручивания нити ш, соотнетствующий определенному усилию F, задаваемому крутильной головкой. Угол поворота цилиндра измеряется по смещению светового луча, испускаемого осветителем 5 и отражаемого зеркальцем 6 иа шкалу 7.
Описанный прибор весьма удобен для исследования кинетики развития деформации сдвига после приложения заданного постоянного напряжения и кинетики спада деформации после разгрузки.
А. А. Трапезниковым сконструирован прибор, названный комплексным эла — стовискозиметром. Он позноляет применять различные рабочие ячейки (коаксиальные цилиндры, конус, диск) и использовать самые разнообразные методы исследования.
Более подробно методы определения упруго-пластических свойств структурированных коллоидных и микрогетерогеииых систем рассматриваются в руководствах к практическим занятиям по коллоидной химии
 1 ноября, 2012
1 ноября, 2012  admin
admin 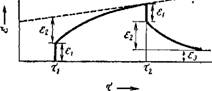
 Опубликовано в рубрике
Опубликовано в рубрике 