Как указывалось выше, структурированные системы не подчиняются закону Ньютона. Это может быть обусловлено либо наличием в жидкости несвязанных друг с другом обрывков структуры, либо малопрочной "сплошной структурной сеткой, способной разрушаться при действии на систему сравнительно малых усилий.
В первом случае система ведет себя при течении как жидкость, в которой взвешены частицы, способные ориентироваться или деформироваться. Обрывки структурной сетки разрушаются в результате различной скорости слоев в потоке, а отдельные элементы разрушенной сетки, если они имеют вытянутую форму, ориентируются своей длинной осью по направлению течения.
Второй случай более сложен. Сначала Ф. Н. Шведов, затем Бингам предположили, что течение системы с малопрочной пространственной структурой начнется лишь тогда, когда напряжение сдвига Р превысит какое-то определенное критическое значение 0, необходимое для разрушения структуры, т. е. когда начнет соблю-. даться условие Р — 0 > 0. Такое течение Бингам называет пластическим, а критическое (предельное) напряжение сдвига 0 —> Пределом текучести.
Очевидно, что для систем с пластическим течением уравнение Ньютона должно быть заменено уравнением Бингама:
Р — 8 = г)’ (du/dx)
Или
— Р = r‘ (du/dx) + 9 (X, 9)
Где г)’ — вязкость, отвечающая пластическому течению системы (пластическая вязкость).
При отсутствии структурной сетки значение 0, очевидно, равно нулю и уравнение Бингама переходит в уравнение Ньютона, а пластическая вязкость т)’ — в истинную вязкость жидкости. Бингам принимает, что как только Р превысит 6 и начнется течение, вязкость системы сразу принимает постоянное значение. При таких
|
Рис. X, 6. Зависимость между Du/Dx И Р для реальной пластической системы. |
|
Рнс. X, 5. Зависимость между Du/Dx и Р для пластической системы по Бннгаму. |
|
•3 |
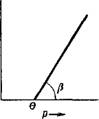
Условиях зависимость du/dx от Р выразится прямой линией (рис. X, 5). Согласно этому рисунку пластическую вязкость можно выразить так:
Где р — угол, образуемый прямой с осью абсцисс.
Примером систем, довольно хорошо подчиняющихся уравнению Бингама, могут служить пасты из глины и консистентные смазки. Однако для большинства структурированных коллоидных систем зависимость du/dx от Р выражается не прямой, а кривой (рис. X, 6). Причина такого явления заключается в том, что при достижении предела текучести структура разрушается не сразу, а постепенно по мере увеличения градиента скорости движения жидкости. Очевидно, можно различать три критических напряжения сдвига: 1) 6/ — первый, или минимальный, предел текучести, соответствующий началу течения (началу разрушения структуры); 2) 0В — предел текучести по Бингаму, отвечающий отрезку на оси абсцисс, отсекаемому продолжением прямолинейного участка кривой; 3) 0Макс — максимальный предел текучести, соответствующий значению Р, при котором кривая переходит в прямую линию.
Очевидно, бмакс представляет собой то напряжение, при котором структура в жидкости разрушается полностью. Все три предела являются характеристикой механических свойств структуры, существующей в системе.
В последние годы структурная вязкость коллоидных систем была детально изучена П. А. Ребиндером и его школой, а также
А. А. Трапезниковым с сотр. В результате — этих работ было показано, что при любок скорости течения в коагуляционной структуре протекают два противоположных процесса — разрушение и восстановление. Равновесное состояние между этими процессами в установившемся потоке характеризуется эффективной вязкостью.
При малых скоростях течения системе — наносятся незначительные повреждения* так как разрушения, неразрывно связанные с течением, успевают тиксотропно восстановиться вследствие медленности процесса течения и течение системы происходит практически без разрушения структуры, т. е„ наблюдается явление ползучести.
При больших скоростях течения структура системы значительно разрушается; при этом разрушенная структура из-за быстроты процесса восстанавливается незначительно.
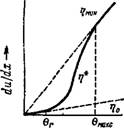
Для характеристики течения структурированных жидкостей и пластичных тел следует использовать не пластическую, а эффективную вязкость г)*, которая уменьшается с ростом действующего напряжения сдвига в системе. При малых напряжениях: сдвига эффективная вязкость имеет наибольшее значение, равное тід вязкости жидкости с практически неразрушенной структурой. При больших напряжениях сдвига эффективная вязкость уменьшается до предельного значения т)Мин — вязкости, отвечающей полному разрушению структуры (при условии сохранения ламинарности потока).
Кривые течения (Du/dx, Р) и зависимость вязкости от напря— жения сдвига для структурированных систем, по П. А. Ребиндеру,. имеют вид, изображенный на рис. X, 7.
|
|
Вязкость структурированных коллоидных систем сильно зависит от условий ее определения, в частности от градиента скорости, пр№ котором она измеряется. Поэтому значения вязкости таких систем можно сравнивать только тогда, когда они найдены в таких, состояниях, которые характеризуются одинаковыми значениями
числа Рейнольдса. Кроме того, по тем же соображениям вязкость золей целесообразно определять не при каком-нибудь одном напряжении сдвига, а необходимо получать кривые du/dx, Р, характеризующие реологические свойства системы в достаточно большом интервале значений Р. Однако даже при измерении в совершенно одинаковых условиях с использованием одного и того же •вискозиметра найденные значения вязкости для какой-нибудь определенной системы могут существенно различаться в зависимости ■от предыстории системы и от того, когда система была приготовлена. Так, при достаточно длительном стоянии коллоидной системы вязкость ее может постепенно повышаться благодаря процессу структурирования. Такое изменение вязкости можно наблюдать на золях гидрата окиси железа или пятиокиси ванадия. С другой стороны, в результате механического воздействия, например при протекании систем через капилляр, структуры, образовавшиеся в системе, могут разрушаться, вследствие чего вязкость ее уменьшается. Именно этим объясняется то обстоятельство, что яри следующих непосредственно друг за другом измерениях вязкости с помощью капиллярного вискозиметра очень часто получают непрерывно уменьшающиеся значения, стремящиеся к определенному пределу.
 1 ноября, 2012
1 ноября, 2012  admin
admin 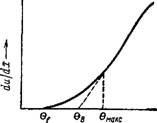
 Опубликовано в рубрике
Опубликовано в рубрике 