Значение ^-потенциала можно вычислить по уравнению (VII, 44). Для этого необходимо измерить скорость электрофоре — тического передвижения частиц в системе при известном градиенте потенциала прилагаемого напряжения и знать значения вязкости и диэлектрической проницаемости жидкости.
|
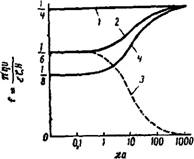
Рис. VII, 20. Влияние концентрации с электролита в растворе ка электрокинетические свойства системы: / — изменение диэлектрической проницаемости е; 2— изменение ^-потенциала, вычисленного без учета изменения е; 3— изменение £-потенциала, вычисленного с учетом изменения е; 4—изменение электрофоретической подвижности и. |
Однако прежде чем рассматривать экспериментальные методы определения скорости электрофоретического переноса, остановимся на различного рода ограничениях, которые надо иметь в виду при применении уравнений (VII, 42) и (VII, 44).
Согласно исходным положениям, электрофорез представляет собой явление, близкое электроосмосу. И для электрофореза, и "для электроосмоса, как мы приняли ранее, перемещение жидкости по отношению к поверхности твердой фазы определяется силами, действующими на двойной электрический слой. Именно исходя из этих предпосылок нами и было выведено уравнение Гельмгольца — Смолуховского, выражающее зависимость скорости электрофореза от градиента потенциала внешнего поля. Однако применение уравнения (VII, 42) для описания электрофоретических явлений ограничено следующими условиями. Во-первых, толщина двойного слоя (обычно характеризуемая величиной 1/х) должна быть мала по сравнению с размером частицы. Во-вторых, вещество частицы не должно проводить электричества, а поверхностная проводимость на межфазной границе должна быть настолько малой, чтобы она практически не влияла на распределение внешнего электрического поля.
Длительное время уравнение Гельмгольца — Смолуховского считали справедливым во всех случаях, независимо от того, выполняются ли вышеприведенные условия или нет. Но в 1924 г. Гюк — кель, основываясь на новой теории сильных ‘электролитов, дал другое уравнение, отличающееся от уравнения (VII, 42) численным множителем 2/з:
И = Є£Я/(6яті) (VII, 47)
При выводе этого уравнения коллоидная частица принята эквивалентной сферической частице и введена поправка на так называемое электрофоретическое^ запаздывание (торможение), вызванное влиянием внешнего поля на двойной электрический слой. Под действием этого поля противоионы передвигаются в направлении, противоположном движению частицы, сообщая этим самым движение окружающей жидкости в том же направлении. Это приводит к тому, что частица перемещается не в покоящейся, а в движущейся жидкости, в результа. те чего электрофоретическая скорость уменьшается.
Генри в 1931 г. показал, что уравнения (VII, 42) и (VII, 47) справедливы каждое в отдельном случае. При выводе уравнения (VII, 42) учитывалась деформация электрического поля, вызванная непроводящей частицей, а при выводе уравнения (VII, 47) допускалось, что непроводящие частицы не влияют на поле в двойном слое и объеме жидкости. Последнее предположение справедливо лишь тогда, когда электропроводность частиц равна электропроводности среды или размеры частиц так малы по сравнению с толщиной двойного слоя, что деформация в большей части двойного слоя становится несущественной.
Тщательно рассматривая вопрос с математической точки зрения и принимая во внимание деформацию внешнего поля, Генри показал, что ^скорость электрофореза во всех случаях может быть выражена уравнением
И =/е£Я/(яті) (VII, 48)
Где f^ функция величины ха; а — радиус сферической частицы или длинная ось цилиндрической Частицы; и— величИна, обратная толщине двойного слоя, численно равная */ъпегЫА £ czVbkT.
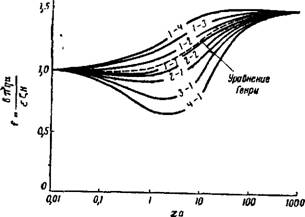
Значение величины F неодинаково для частиц разной формы и различно расположенных по отношению к полю. Зависимость этой величины от ха показана на рис. VII, 21.
Для непроводящих цилиндрических частиц, ось которых совпадает с направлением поля, /= 1/4, как в уравнении (VII, 42). Для цилиндрических частиц, расположенных перпендикулярно направлению поля, F — 1/8 при малых значениях ха в приближается к 1/4 прн больших величинах ха. Для сферических
Частиц F = 1/6 при малых значениях ш и F «= 1/4 при больших значениях этой величины. Таким образом, данные рис. VII, 21 находятся в полном соответствии с уравнением (VII, 42), согласно которому численный коэффициент равен 1/4 независимо от формы частиц, если значение ха велико, н с уравнением (VII, 47), согласно которому численный множитель равен 1/6 для сферических частнц с малым значением на.
Геири проанализировал также влияние на величину F электропроводности дисперсной фазы, полностью меняющей распределение электрического поля вблизи частиц. На рис. VII, 21 пунктиром обозначены значения коэффициента f в зависимости от величины ха для электропроводящих частиц сферической формы. Как и следовало ожидать, распределение поля ве сказывается на величине F при очень большой толщине двойного электрического слоя (Ха < 1), ио с уменьшением толщины слоя коэффициент уменьшается И в пределе становится равным нулю. Однако на практике в большинстве случаев влияние электропроводности коллоидвых частнц металлов можно не учитывать, так как оно почти полностью устраняется поляризацией поверхности. При этом частица ведет себя так, как она должна вести себя, если бы состояла из непроводящего вещества.
Из всего приведенного следует, что для выбора правильного численного коэффициента в уравнении Геири необходимо знать размер частицы а, форму частицы (цилиндр, сфера) и толщину двойного электрического слоя. Необходимо также знать, является ли дисперсная фаза проводником или диэлектриком. Первые две характеристики (размер и форма частицы) определяются экспериментально с помощью оптических и иных методов. Электропроводность дисперсной фазы обычно известна. Толщину двойного электрического слоя, или, что то же, иоиной атмосферы, согласно теории сильных электролитов можно вычислить по уравнению (VII, 5).
|
Рис. VII, 21. Зависимость величины F От ха для частиц: цилиндрическая (ось параллельна полю), ие проводящая ток; 3—йфериче — екая, ие проводящая ток; J—сферическая, проводящая ток; 4—цилиндрическая (ось перпендикулярна полю), не проводящая ток. |
При наложении внешнего электрического поля движущаяся заряженная частица подвергается не только рассмотренному выше электрофоретическому торможению, но и действию так называемой ^электрической релаксации, которая заключается в следующем. Согласно электрической теории электрофореза предполагается, что электрическое поле двойного слоя и внешнее электрическое поле просто накладываются одно на другое. Однако на самом деле этого нет, так как частица и внешняя часть двойного
слоя движутся в противоположных направлениях, и первоначальная симметрия двойного слоя относительно частицы нарушается. Вследствие электропроводности и диффузии двойной слой стремится восстановить симметрию, но это восстановление требует времени (времени релаксации), и поэтому внешняя часть двойного слоя все же остается позади движущейся частицы. В результате этого возникает добавочное электрическое поле, которое действует на частицу, стремясь двигать ее в обратном направлении, и тем самым влияет на скорость электрофореза.
|
|
Рис. VII, 22. Влияние релаксации и различных типов электролитов на электрофорез коллоидных частиц с отрицательным £-потеициа-
Лом, равным 50 мВ. Тип электролита обозначен цифрами у кривых: первая цифра характеризует валентность катиона, вторая—валентность аниона.
Не рассматривая подробно влияние электрической релаксации на скорость электрофореза, отметим лишь, что, согласно Овербеку, эффект релаксации зависит от С-потенциала, величины на и от валентности ионов электролитов, присутствующих в системе. На рис. VII, 22 в качестве иллюстрации показано влияние электрической релаксации для сферических коллоидных частиц с отрицательным ^-потенциалом, равным 50 мВ, и различных типов электролитов. На оси абсцисс отложены значення на, а на оси ординат — зваченвя величины {‘, ва которую следует умножить скорость электрофоретического переноса, вычисленную по уравнению Гюккеля (VII, 47), чтобы получить правильные результаты. Пунктирной линией-показана кривая, характеризующая изменение скорости, вычисленной по уравнению Геири без учета релаксации.
По данным рис. VII, 22 можно сделать вывод о незначительных релаксационных эффектах прн малых н больших значеннях ка. Характерно различное расположение кривых в завнснмостн от электролитов различного типа. Электрофорез отрвцательно заряженных частнц замедляется симметричными электролитами н электролитами, имеющими поливалентные катионы. Наоборот, поливалентные анноны ускоряют электрофорез отрицательно заряженных частиц. »
С увеличением электрокинетнческого потенциала н валентности ионов по* правка на релаксацию быстро возрастает. Но при значеннях электрокинетического потенциала, меньших 25 мВ, нли прн использовании электролитов с одновалентными катионами и анионами релаксационный эффект мал и поправку на
релаксацию в уравнение Генри можно не вводить, так она не превышает в этом случае 3%.
|
|
Помимо явлений электрофоретического запаздывания и электрической релаксации на скорость электрофореза может влиять и агрегатное состояние дисперсной фазы. Так, скорость электрофоретического переноса жидких частиц при всех прочих одинаковых условиях электрофореза равна подвижности твердых частиц лишь в частном случае, когда в результате адсорбции поверхностно — активных веществ поверхность капли становится неподвижной, что делает жидкую частицу похожей на твердую. В общем же случае жидкие частицы, обладающие достаточно высокой проводимостью, движутся при электрофорезе значительно быстрее, чем твердые. Это объясняется следующими причинами. Во — первых, трение о поверхность жидкой частицы всегда меньше, чем трение о поверхность твердого шарика таких же размеров, так как капли жидкости могут деформироваться при движении среды Во-вторых, двойной электрический слой
|
|
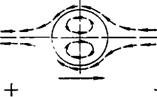
Рис. VII, 23. Движение жидкости в капельке ртути при электрофорезе.
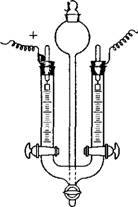
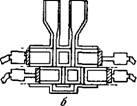
Ркс. VII, 24. Схема -прибора Кёна для электрофореза.
На границе двух жидкостей возникает в обеих фазах, и его часть, приходящая иа каплю, играет существенную роль, заставляя циркулировать жидкость внутри капли, что сказывается на скорости электрофореза.
Следует упомянуть о работах А. Н. Фрумкина, определявшего электрофо — ретическую подвижность капель ртути. А. Н. Фрумкин показал, что капля ртути полностью поляризована, так что ее поведение подобно поведению непроводника. Однако поляризация изменяет поверхностное натяжение на полюсах капли, вызывая движение ртути вдоль поверхности капли. Если капля заряжена положительно (обычный случай), то заряд на поверхности капли у полюса, обращенного к положительному электроду, уменьшается и поверхностное натяжение в этом месте возрастает, тогда как на другом полюсе капли происходит обратное явление. В результате разницы в поверхностных натяжениях внутри капли возникает движение ртути, что схематически представлено на рис. VII, 23. Стрелки внутри капли показывают движение ртути, стрелки снаружи каплн — направление движения дисперсионной среды. Большая стрелка внизу рисунка обозначает направление движения всей капли. Не трудно понять, что это движение ртути должно ускорять перенос частицы к отрицательному электроду. Такие круговые движения могут увеличивать скорость переноса капли на несколько порядков по сравнению с обычными скоростями электрофореза
Рассмотрим теперь кратко основные методы определения скорости электрофореза, уделяя внимание главным образом их принципиальным особенностям, так как технические подробности экспериментальных методик изложены в соответствующих руководствах к практическим занятиям по коллоидной химии. Поскольку
электрофорез во многих отношениях сходен с электролизом, его скорость может быть измерена во многих случаях теми же способами, какими определяется подвижность обычных ионов, например путем определения чисел переноса, измерения скорости перемещения границы раздела, аналитическими методами, а также с помощью микроскопа или ультрамикроскопа.
Метод Гитторфа. Этот метод аналогичен методу, применяемому для определения чисел переноса ионов. Через коллоидный раствор, помещенный в специальный сосуд, пропускают в течение некоторого времени электрический ток и затем в пробах раствора, отобранных из разных мест, аналитически определяют количество дисперсной фазы, переместившейся к одному из электродов. Очевидно, это количество т прямо пропорционально скорости электрофоретического переноса и, концентрации дисперсной фазы с, силе тока / и времени пропускания тока X и обратно пропорционально электропроводности жидкости у, т. е.
M = «с/т/у (VII, 49)
Из этого уравнения можно определить скорость электрофореза:
И — m/(clx) (VII, 50)
Этот метод в применении к коллоидным системам особенно точен благодаря большой массе дисперсной фазы, приходящейся на единицу заряда Однако этот способ применяется на практике довольно редко. Таттье использовал метод Гитторфа не только для определения электрофоретической скорости, но и для одновременного определения-подвижности противоионов.
Метод подвижной границы. Этот метод получил особенно широкое распространение на практике благодаря относительной простоте. Принцип его основан на наблюдении за скоростью передвижения под влиянием электрического поля границы между обычно мутным или окрашенным коллоидным растворам—-и прозрачной бесцветной специальной «боковой жидкостью». Для исследования прозрачного бесцветного золя -используют специальные приемы, способствующие проявлению границы, например освещение ультрафиолетовым светом.
В разное время исследователями было предложено много приборов для осуществления метода подвижной границы. Одним из таких приборов, очень простым по устройству, является прибор Кёна, изображенный на рис. VII, 24. Этот прибор представляет собой широкую стеклянную U-образную трубку, каждое колено которой имеет внизу стеклянный кран с диаметром отверстия, равным внутреннему диаметру трубки. Верхние части обоих колен трубки отградуированы, причем большое деление равно 1 см. В оба колена U-образной трубки вставляются платиновые электроды. Коллоидный раствор можно вводить в прибор с помощью специальной воронки, соединенной с нижней частью U-образной трубки узкой стеклянной трубкой с краном.
Прибор собирают для работы следующим образом. В нижнюю часть U-образной трубки при открытых кранах с помощью воронки вводят исследуемый коллоидный раствор в таком количестве, чтобы его уровень оказался несколько выше кранов. Затем закрывают краны на обоих коленах U-образной трубки и кран на трубке, соединяющий прибор с воронкой. С помощью пипетки (или наклоняя весь прибор) из обоих колен удаляют жидкость, находящуюся над кранами. После этого в оба колена с помощью пипетки вводят определенные количества «боковой жидкости» так, чтобы уровни ее в коленах U-образиой трубки находились на одной высоте и были на 3—4 см выше градуировки. Далее в каждое колено вставляют укрепленный на резиновой пробке электрод и осторожно открывают краны в обоих коленах. В таком виде прибор готов. для работы.
Определение сводится к измерению времени (с помощью секундомера), за которое в одном нз колен трубки после включення постоянного тока определенной силы граница раздела коллоидная система — боковая жидкость передвинется на высоту 1 см. Проводят несколько таких определений, не выключая тока, н для вычисления скорости электрофореза берут нз ннх среднеарифметическое значение. Одновременно с измерением времени с помвщью вольтметра, включенного параллельно в электрическую цепь, отмечают напряжение тока на электродах. В конце работы необходимо измерить также расстояние между обоимн электродами по длине трубкн; это расстояние нужно для вычисления ‘значення градиента потенциала внешнего поля.
В более совершенных приборах боковые колена градуированы как над кранами, так н под ннмн, что позволяет работать с коллоидными системами менее плотными, чем боковая жидкость. Это особенно важно прн работе с эмульсиями, у которых плотность днспёрсной фазы (обычно углеводорода), как правило, меньше плотности дисперсионной среды (воды). При этом боковая жидкость помещается внизу, а коллоидный раствор — вверху.
Для устранения влияния поляризации электродов применяют неполярнзую — щнеся электроды. Для того чтобы в систему не проникали продукты электролиза, электроды обычно помещают в отдельные широкие сосуды, соединяемые с коленамн прибора прн помощи стеклянных трубок, заполненных агаровым студнем, содержащим хлорнд калия, как это принято в электрохимии прн определении рН.
Для большей точности передвижение границы системы коллоидный раствор — боковая жидкость можно наблюдать с помощью короткофокусной оптической трубы, укрепленной на катетометре.
При выборе боковой жидкости следует руководствоваться некоторыми требованиями к ее составу и свойствам. Помимо того, что в отличие от коллоидного раствора она должна быть прозрачной или бесцветной, она должна также не влиять на ^-потенциал переходящих в нее из золя коллоидных частиц и обладать электропроводностью, равной или немного большей электропроводности коллоидной системы. Это обычно обеспечивает образование резкой границы между золем — и боковой жидкостью и позволяет обходиться без введения поправок на их различную электропроводность при вычислении градиента внешнего потенциала.
В качестве боковой жидкости часто применяют ультрафильтрат золя или дисперсионную среду, полученную коагуляцией коллоидной системы путем замораживания. Однако если исследуют относительно концентрированные коллоидные растворы с небольшим содержанием электролитов, приготовленная таким способом боковая жидкость обладает все же несколько иной электропроводностью по сравнению с золем. В этом случае при вычислении скорости электрофореза необходимо — вводить поправки на распределение напряженности в электрическом поле, что подчас бывает трудно.
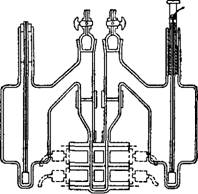
Метод Тизелиуса. Этот метод в принципе сводится к методу подвижной границы, однако в нем много специфических особенностей. Измерения по этому методу проводят в приборе, который представляет собою усовершенствованный аппарат Кёиа. Для создания резкой границы между коллоидным раствором н боковой жидкостью в приборе Тнзелнуса используют не краны, а сдвнг пришлифованных частей U-образной трубкн относительно друг друга. На рнс. VII, 25 дан разрез основной части прибора, соответствующей U-образной трубке прибора Кёна. Нижняк часть трубкн в момент наполнения верхней части боковой
жидкостью должна быть уже заполнена испытуемым золем. Поперечное сеченне U-образнон трубкн имеет не круглую, а прямоугольную форму, что облегчает наблюдение за передвижением границы. Кроме того, в таких условиях жидкость быстрее принимает температуру водяного термостата, являющегося необходимой частью прибора Определения проводят, как правило, прн +4 °С, что соответствует максимальной плотности воды. В этих условиях прн небольших температурных колебаниях плотность жндкостн изменяется весьма мало, поэтому
|
|
Рис. VII, 25. Внд (сбоку) U-образной трубки в приборе Тнзелиуса:
А—рабочее положение, б— положение в ыонеит заполнения верхней части
|
VII, 26 показан прибор Тнзелнуса в |
|
Рис. VII, 26. Схема прибора Тнзелнуса в собранном внде. |
Трубки.
Исключается образование конвекционных токов н размывание границы раздела незначительное Электроды, с помощью которых создается внешнее электрическое поле, расположены в боковых широких сосудах, благодаря чему продукты электролиза не попадают в золь На рнс собранном внде. Передвижение границы определяют по различию в коэффициенте преломления исследуемого раствора н его ультрафильтрата, который обычно используют в качестве боковой жидкости.
Очень остроумная оптическая система Фнльпота — Свенссона позволяет характеризовать распределение градиента коэффициента преломления в области подвижной границы графическим способом Этим методом, прн котором фото — _ графируют нли наблюдают плоский световой луч, проходящий через U-образную трубку, можно регистрировать все неравномерности распределения коллоидного вещества в столбике жидкости. Если градиент коэффициента преломления отсутствует, световой луч благодаря особому устройству линз дает на фотопластинке одну сплошную вертикальную линию Еслн имеется такой градиент, то на фотопластинке ему будет соответствовать пнк. По характеру этого пнка можно судить о положении границы раздела в столбике жидкости, о резкости границы и о разности концентраций по обе стороны от границы раздела.
|
|
Метод Тнзелнуса особенно шнрокапри меняется прн исследовании белков и других высокомолекулярных электролитов, поскольку с его помощью можно не только определить скорость электрофореза, но и разделить смесь высокомолекулярных веществ на отдельные компоненты. В самом деле, если исследуемый раствор содержит нескблько компонентов с различными электрофоретнческнмн подвижностямн, то фронт передвижения более подвижных компонентов будет обгонять фронт движения компонентов, движущихся медленнее, и образуется столько границ, сколько компонентов в смеси.
Электрофорез на бумаге. Прибор Тизелиуса очень сложен. В последнее время широкое распространение для исследования белков получил другой метод, предложенный также Тизелиусом, но осуществляемый проще. Это метод электрофореза на бумаге.
Он выполняется следующим образом. На середину полоски плотной, гомогенной фильтровальной (хроматографической) бумаги, пропитанной буферным раствором с определенным значением рН, наносят каплю исследуемого коллоидного раствора. Затем на полоску бумаги накладывают разность потенциалов. Под влиянием образующегося электрического поля отдельные компоненты, содержащиеся в капле, обладающие разными электрофоретическими подвижностя — ми, передвигаются по полоске с различными скоростями. Через некоторое время компоненты распределяются на бумаге в виде стольких зон, различно удаленных от исходной точки, сколько компонентов содержалось в растворе. Полоску высушивают и прогревают для денатурации и фиксации находящихся на ней белков и после этого окрашивают подходящими красителями. В результате проявляется распределение компонентов по длине полоски. Роль бумаги в этом методе сводится к устранению диффузионного и конвекционного перемешивания белков при электрофорезе.
Методом электрофореза на бумаге можно не только исследовать состав смесей высокомолекулярных веществ, но и выделить отдельные компоненты. С этой целью полоску бумаги, не прогревая, разрезают на части и из них экстрагируют отдельные, уже разделенные компоненты. Теория этого метода, при котором существенную роль играют поверхностные и адсорбционные явления, еще мало разработана.
Микроскопический и ультрамикроскопический методы. Эти методы определения электрофоретической подвижности заключаются В определении скорости передвижения индивидуальных коллоидных частиц в электрическом поле при помощи микроскопа или ультрамикроскопа. Преимущество этого метода перед методом по — дв’ижной границы состоит в том, что при исследовании с помощью микроскопа частицы находятся в одной и той же окружающей их среде и отсутствует поверхность раздела между коллоидной системой и боковой жидкостью. Другое преимущество этого метода заключается в том, что для определения достаточно очень малое количество раствора. Недостаток этого метода тот, что нельзя исследовать электрофоретическую подвижность частиц в растворах С более или менее значительной концентрацией дисперсной фазы, так как в таких растворах наблюдение за перемещением отдельной частицы невозможно. Разбавление же системы чужеродной жидкостью всегда влияет на ^-потенциал.
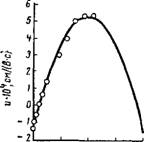
При микроскопическом или ультрамикроскопическом методе испытуемый коллоидный раствор помещают в снабженную электродами закрытую кювету с прямоугольным или цилиндрическим сечением и измеряют время, необходимое для того, чтобы выбранная частица передвинулась на определенное расстояние. Так как частицы находятся в броуновском движении, то необходимо брать среднее арифметическое значение из многих таких определений. Кроме того, следует учитывать, что жидкость в кювете находится в движении в результате электроосмотического перемещения вдоль стенок кюветы. Однако вследствие того, что кювета закрыта, в центре кюветы устанавливается обратный ток жидкости, и, таким образом, перенос жидкости в кювете в целом равен нулю. Скордсхь-авй-_ жения жидкости в кювете налагается на электрофоретическую скорость движения частиц, и найденное значение представляет алгебраическую сумму этих скоростей. Понятно, что значение этой суммы сильно зависит от местонахождения частицы в кювете. Примером этому могут служить результаты работы Эллиса,
определившего зависимость между скоростью движения масляных капель в кювете с прямоугольным сечением и высотой, на которой находились капельки относительно дна кюветы. Эти данные представлены в виде точек на рис. VII, 27 (парабола на рисунке соответствует теоретически вычисленной скорости электрофореза).
Для вычисления истинной электрофоретической скорости можно взять среднее значение наблюдаемых скоростей по всей плоскости поперечного сечения кюветы. Однако это сложно, и практически проще измерять электрофоретическую скорость в том месте поперечного сечения кюветы, где скорости электроосмоса и обратных потоков равны друг другу и где вследствие этого жидкость находится в покое Теория, с помощью которой находятся такие места в кювете, дана Смолуховским, она приводится в практикумах по коллоидной химии. Здесь
|
О 0,5 1,0 Отн. гпубина кюбеты |
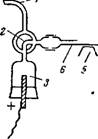
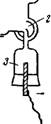
Рис. VII, 27. Наблюдаемая (точки) и вычисленная (кривая) скзрости электрофоретического переноса масляных капель на различной глубине кюветы.
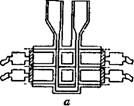
Рис. VII, 28. Схема прибора, предложенного Абрамсоном для микроэлектрофореза: /— воронка для исследуемого раствора; 2— трехходовые краны; 3 — неполяризую — щиеся электроды; 4 —объектив микроскопа; 5 — коидеисор; 6— кювета; 7 — трубка для отвода раствора.
Же укажем лишь, что для кюветы с круглым сечением слой, где скорость движения жидкости равна нулю, лежит на расстоянии 0,148 диаметра от стенки. Для плоской кюветы большой ширины таких слоев два, причем каждый из них находится на расстоянии, равном 0,212 от ее высоты. Иначе говоря, эти слои соответствуют примерно 1/5 и 4/5 высоты кюветы.
Для микроскопического и ультрамикроскопического определения электрофоретической скорости предложен ряд приспособлений и приборов. Простейшие из них представляют собой кюветы, состоящие из предметного и покровного стекла, между которыми помещают две тонкие платиновые пластинки, приклеенные к обоим стеклам и служащие электродами. После введения золя в эту кювету боковые щели ее замазывают вазелином. Понятно, что при работе с такими кюветами не исключается поляризация электродов и переход продуктов электролиза в золь.
На рис. VII,28 дана схема прибора для микроэлектрофореза, предложенного Абрамсоном. Этот прибор состоит из плоской стеклянной кюветы 6, переходящей в стеклянные трубки, заканчивающиеся трехходовыми кранами 2. Один нз этих кранов соединяет кювету с воронкой I. Пользуясь воронкой и кранами, вначале кювету промывают, а затем наполняют исследуемым коллоидным
раствором. Непосредственно перед измерением, поворачивай краны, кювету отсоединяют от воронки и сливиой трубки 7 и соедиииют с иеполиризующимиси электродами 3 цинковыми палочками в насыщенном растворе сульфата циика.
Как правило, электрофорез проводят при постоянном токе, причем в электрическую цепь прибора вводят переключатель для перемены направления тока. Интересно, что Сведберг еще в 1919 г. использовал для определении электро — форетической скорости переменный ток, при котором частицы совершают колебания и видны в ультрамикроскопе с темным полем как светлые линии определенной длины. Зная частоту тока и измерив длину светлой линии, можно вычислить электрофоретическую скорость.
В заключение следует указать, что описанный метод определения электрофоретической подвижности можно применять и к растворам высокомолекулярных соединений, отдельные молекулы которых в ультрамикроскопе не видимы. Для этого в раствор вводят малые частицы кварца или угля, которые адсорбируют на себе высокомолекулярное вещество. Как показали многие эксперименты, электрофоретическая подвижность таких частиц такая же, как и подвижность свободных макромолекул. Это становится понятным, если учесть, что электрофоретическая скорость, согласно уравнению Гельмгольца — Смолуховского, не зависит от размера частиц. Однако всегда следует помнить, что ^-потенциал, вычисленный по результатам таких измерений, является в некоторой степени фиктивной величиной, так как в этом случае довольно трудно представить себе наличие двойного слоя с более или менее постоянным потенциалом.
Как мы уже зиаем, С-потеицнал можно вычислить ие только по скорости электрофореза, но и по электроосмотической скорости передвижении. Хотя прямое определение электроосмотической скорости возможно, гораздо удобнее для вычислении С-потенциала измерять объем жидкости, проходящий при электроосмосе через капиллир или пористую мембрану, или давление, развивающееся в результате электроосмотического движения жидкости.
Определение по объему электроосмотически перенесенной жидкости. Дли объема жидкости V, протекающего через одиночный капиллир радиуса г в единицу времени, очевидно, справедливо выражение:
Y.^^L. I^L (VII.51)
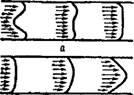
Следует помнить, что при электроосмотическом течении жидкости через капилляр движущая сила имеет электрическую природу и она действует на периферические части цилиндра жидкости, заполняющей капилляр, где сосредоточены свободные противоионы. В результате этого при наложении электрического поля скорость движения жидкости в капилляре будет сначала максимальной у стенки капиллира и минимальной у его оси. Затем, вследствие трения между слоями жидкости, скорости выравниваются и при стационарном режиме течения жидкость движется практически с одинаковой скоростью по всему течению капилляра. Схема, иллюстрирующая установление стационарного течения при электроосмосе, приведена иа рис. VII, 29а.
При электроосмосе характер движении жидкости прямо противоположен тому, который наблюдалси бы при движении жидкости под влиянием гидростатического давления, когда в начале течения скорости жидкости всюду равны. Однако в последнем случае постепенно начинает сказыватьси трение у стенки,
скорость течения периферийных слоев становится меньше, чем центральных, и, наконец, эпюра скоростей при стационарном режиме течения принимает форму параболы (рис. VII,296).
Пористую мембрану, согласно Смолухонскому, можно рассматривать как сумму капилляров с общей площадью сечеиия s. Тогда объем жидкости, элек — троосмотически протекающей в единицу времени через мембрану, будет выражаться следующим уравнением:
V = = —(VII, 52>
Таким образом, объем жидкости, электроосмотически перенесенной через мембрану, прямо пропорционален поперечному сечению капилляров, диэлектрической проницаемости, ^-потенциалу, приложенной электродвижущей силе и обратно пропорционален вязкости жидкости.
Согласно закону Ома:
£ = (VII, 53)
Где Е — приложенная разность потенциалов; I — сила тока; R — электрическое сопротивление системы. Электрическое сопротивление раствора электролита равно: — .
L &
(VII, 54)
Ys Рис. VII, 29. Схема, пояс
Няющая установление-
Где L — толщина слоя раствора; S — площадь сече — стационарного режима ния; у —удельная электмпооводиость раствора. Под — течения жидкости в ка — ставляя в уравнение (VII, 53) приведеииое выраже — пилляре:
НИЄ для R, получим: о—при электроосмосе; в—под
IL ,,„, „. действием гидростатического
£=«//<«= —— (VII, 55) давления.
УS
Пользуясь этим выражением для Е, градиент внешнего потенциала можно выразить следующим образом:
Я = (VII,56>
L syL Уs Г
Подставляя найденное значение градиента в уравнение (VII,52), имеем:
|
(VII, 57> |
.. szH seЈI Е£/
4як) 4лт)у5 4ят)у
Так как в уравнение (VII, 57) не входит ии L, ии S, то, очевидно, при постоянной силе тока объем жидкости, прошедший сквозь мембрану, ие зависит от поперечного сечения и длины капилляров. Правильность уравнения (VII, 57) была подтверждена опытами Видемана.
Из уравнения (VII, 57) легко найти значение С-потеициала:
(VII,58>
По аналогии с уравнением (VII, 46) правую часть этого уравнения надо умножить на 3002 для того, чтобы ^-потенциал был выражен в вольтах. Тогда уравнение (VII, 58) будет иметь вид:
4ЛТ"е7°°г (VII,59)
|
|
Таким образом, для того чтобы определить значение J-потенциала по электроосмосу, следует экспериментально определить объем жидкости, перенесенной
•через капилляр или пористую мембрану, удельную электропроводность раствора и силу тока, при которой проводился электроосмос. Остальные величины берут -обычно из справочников.
При использовании уравнения (VII, 58) необходимо учитывать возможность явления так называемой поверхностной проводимости. Это явление сводится к тому, что находящиеся около межфазной границы ионы изменяют состав среды, а следовательно, и удельную электропроводность раствора у межфазиой границы. Если радиус капилляра достаточно велик по сравнению с толщиной слоя у стенки, где проявляется поверхностная проводимость, средняя электропроводность раствора остается приблизительно той же, что и в его объеме, и вели — «чина у в уравнении (VII, 58) является удельной электропроводностью раствора.
|
О 50 100 Г, мкм |
Рис. VII, 30. Зависимость ^-потенциала от радиуса капилляра г С учетом (/) н без учета (2) поверхностной проводимости: Л—мембрана нз кварца; 5—мембрана нз корунда.
ТЗсли же капилляры тонкие, это условие не соблюдается и у становится уже функцией радиуса капилляра. В этом случае вместо уравнения (VII, 58) следует .пользоваться уравнением:
^4nn(y-+Oys/s)V (Vn>60)
•где О — длина окружности капилляра; s — его сечение; у*— поверхностная проводимость.
Множитель (у + Oy>/S) в числителе уравнения (VII, 60) ставится вместо величины у. исходя из следующих соображений. Электропроводность жидкости, заполняющей капилляр, Y равна сумме электропроводностей (обратных сопротивлений) объемной части жидкости и приповерхностного слоя:
L/R=/R+/Rs (VII, 61)
Где 1IR = Ys/L, L/R — Ys/L и L/R, = Ys O/L, причем принимается, что толщина слоя с поверхностной проводимостью мала по сравнению с радиусом капилляра. Отсюда общая электропроводность у равна
Y = Y + -^ (VII, 62)
Величина Ov’s/s, очевидно, представляет собой увеличение электропроводно — — сти жидкости в капилляре в результате поверхностной проводимости. Так как O/S ~ 1/г, то поправка на поверхностную проводимость не нужна при капиллярах достаточно большого радиуса.
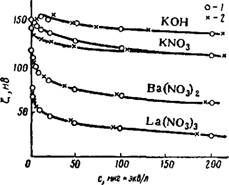
Сравнивая уравнения (VII, 58) и (VII, 60) и учитывая, что величина Oys/S Всегда положительна, можно видеть, что вследствие поверхностной проводимости истинные значения С-потенциала при достаточно тонких капиллярах всегда выше вычисленных без введения поправки на поверхностную проводимость. Эксперименты подтвердили это положение. На рис. VII, 30 приведены резуль — тэты опытов И. И. Жукова по определению С-потенциала протекания, вычисленные с учетом (кривые 1) и без учета (кривые 2) поверхностной проводимости. В качестве пористых мембран были взяты диафрагмы из кварца и корунда, в качестве жидкости — слабый раствор хлорида калия. По характеру кривых видно, что значения С-потенциала без учета поверхностной проводимости сильно уменьшаются при переходе к диафрагмам с порами малого сечения, а при введении поправки иа поверхностную проводимость получаются почти одни и те же — значения электрокинетического потенциала во всем испытанном диапазоне радиусов капилляров. Следовательно, при определении С-потенциала электроосмотическим путем нли методом протекания необходимо всегда учитывать радиус пор- капилляров.
Приведенная выше поправка характеризует поверхностную проводимость только отдельного капилляра, тогда как на практике в большинстве случаев, реальными объектами являются пориыые тела. Для определения поправки на
|
|
|
2 1 2
Рис. VII, 31. Схема прибора Перрена для электроосмоса: 1 — порошок исследуемого вещества; 2— электроды; 3— вороика; 4 — кран; 5 — прокалиброванная трубка. |
Поверхностную проводимость пористых тел измеряют электросопротивление — мембраны в исследуемом и стандартном растворах и по этим данным вычисляют величину Ys-
С поверхностной проводимостью связано явление так называемой капиллярной сверхпроводимости. Это явление, открытое Д. А. Фридрихсбергом, заключается в следующем. Если трубку с проводящим ток раствором перегородить пористой диафрагмой из непроводящего материала, то электрическое сопротивление системы должно возрасти вследствие того, что часть сечения трубки будет занята диэлектриком. Однако если у поверхности капилляров диафрагмы образуется слой, обладающий поверхностной проводимостью, то за счет этой проводимости для весьма тонкокапиллярных пористых тел в разбавленных растворах электролитов может наблюдаться повышение общей проводимости. Будет иметь место на первый взгляд парадоксальный эффект понижения электрического сопротивления при введении в трубку диафрагмы из диэлектрика.
Остановимся теперь кратко на приборах, применяемых для определения С-потенциала по объему электроосмотически перенесенной жидкости. Во всех приборах этого типа электроосмос проводится не с одиночным капилляром, а с помощью пористой диафрагмы из твердого вещества.
На рис. VII, 31 приведена схема прибора для электроосмоса, предложенного еще Перреном. В среднюю часть стеклянной U-образной трубки, присоединяемой к боковым коленам с помощью шлифов, набивают достаточно плотно порошок 1 исследуемого вещества. В оба боковых колена вставлены платиновые электроды 2, питаемые постоянным током, напряжение которого должно составлять не менее 40—50В. В правом боковом колене имеется воронка 3 с краном для заполнения прибора дисперсионной средой, а в левом колене — кран 4 для слива
жидкости из прибора. Кроме того, к правому колену трубки присоединена капиллярная горизонтальная заранее прокалиброванная трубка 5, служащая для наблюдения за перемещением в ней жидкости.
Перед определением прибор заполняют жидкостью так, чтобы в порах диафрагмы / не оставалось воздуха и установилось постоянное положение мениска жидкости в левой части капиллярной трубки 5. После этого включают ток в таком направлении, чтобы мениск в капилляре 5 передвигался слева направо, и отсчитывают скорость его перемещения по секундомеру. Одновременно с помощью миллиамперметра, включенного в электрическую цепь прибора, измеряют силу тока. Недостатком прибора является поляризация электродов и образование продуктов электролиза, которые могут проникать в капилляры диафрагмы и этим самым вносить ошибку в результаты измерения.
В’ более совершенных приборах применяют иеполяризующиеся электроды, достаточно удаленные от диафрагмы или соединенные с ней с помощью агаровых мостиков. В приборе для электроосмоса, предложенном Уметсу, диафрагма из порошка располагается в вертикальной стеклянной трубке со стеклянной решеткой в нижней ее части.
Диафрагму необходимой высоты получают, наполняя трубку суспензией порошка н отсасывая затем жидкость водоструйным насосом. После этого прибор заполняют раствором, вставляют агаровые мостики для соединения диафрагмы с неполяризующимися электродами и включают постоянный электрический ток. Скорость электроосмоса определяют с помощью калиброванного стеклянного капилляра, при этом начальное положение мениска жидкости устанавливают, приоткрывая специальный боковой кран.
Определение по электроосмотическому давлению. При этом способе определяют не объем жидкости, протекшей при электроосмосе через капилляр или пористую мембрану в единицу времени, а давление, возникающее в результате электроосмотического движения жидкости. Для этого то колено электроосмотического прибора, в которое поступает жидкость, должно заканчиваться вертикальной или наклонной трубкой, с помощью которой можно установить высоту столба жидкости, уравновешивающего электроосмотическую силу. Давление этого столба заставляет жидкость течь через капилляр или пористую мембрану в обратном направлении, пока не установится равновесие между-силой тяжести и ■осмотическим давлением.
Уравнение, с помощью которого можно вычислить С-потенциал, выводят, исходя из того, что в равновесном состоянии объем жидкости Vi, поступающей в отдельный капилляр в единицу времени под влиянием электроосмотической силы, равен объему жидкости V2, вытекающему за то же время из капилляра под влиянием гидростатического давления Р. Объем Vi выражается уравнением (VII, 51):
V^S^L
4т]
Для Vi, согласно уравнению Пуазейля, можно написать:
|
8щ/ След Г2 г1Н пРг♦ |
ПРг*
Где I — длина капилляра.
В равновесном состоянии Vt = V2 и, следовательно:
(VII, 63)
4т) 8т|/ Откуда
P = (Vii, 64)
Яг2
Еще Квинке и Видеман нашлн, что электроосмотическое давление Р пропорционально градиенту внешнего потенциала Н и обратно пропорционально гг, что полностью соответствует уравнению (VII, 64).
Из уравнения (VII, 64) легко иайти значение С-потеициала по давлению Р или высоте поднятия жидкости в трубке.
Подобный метод можно применить (в отсутствие поверхностной проводимости) также и при электроосмосе через пористую мембрану. Однако он не получил широкого распространения иа практике.
Сравнение значений ^-потенциала, найденных ‘ различными методами
Из изложенного выше ясно, что определение электрокинетического потенциала сопряжено со многими трудностями, связанными как с постановкой эксперимента, так и с вычислением ^-потенциала по экспериментальным. данным. Еще сравнительно недавно исследователи не учитывали влияния поверхностной проводимости, электрофоретиче — ского запаздывания и электрической релаксации, и поэтому нз большого числа исследований в области электрокннети — ческих явлений лишь немногие давали достоверные значения ^-потенциала.
Наилучшим доказательством точности значений £-по — тенциала, определяемых с учетом нужных поправок, может служит^ идентичность его значений, найденных при различных электрокинетических явлениях.
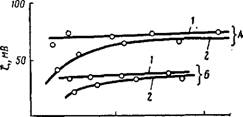
Опыты, проведенные Рат — джерсом, а также Вьигом с целью сравнения значений ^-потенциала, определенного методом протекания и по электроосмвсу, показали одинаковость этих значений. На рис. VII, 32 представлена зависимость между £-потен — циалом стенки стеклянного капилляра и концентрацией раствора электролита, заполняющей» капилляр. Как можно видеть, значения ^-потенциала, вычисленные из электроосмотических данных и из данных, полученных при определении потенциала протекания, ложатся на одну и ту же кривую. Расхождения данных для KNOj объясняются другой обработкой капилляра, примененного в этом опыте.
|
Рис. VII, 32. Заиисимость {-потенциала стенки капилляра из стекла пирекс от Концентрации электролита: 1—данные, вычисленные по реаультатам электроосмотических определенна; 2—данные, полученные прн определения потенциалов течения. |
Эквивалентность значений ^-потенциала, найденных с помощью электрофореза и электроосмоса, также неоднократно проверялась. В частности, Абрамсон в своих тщательных опытах по исследованию электроосмоса и микроэлектрофореза покрытых белком частиц при учете всех необходимых поправок установил равенство
значений ^-потенциала, найденных обоими способами. Наконец, ^-потенциал, определенный по методу протекания, оказался равным ^-потенциалу, вычисленному из электрофоретических данных.
Таким образом, хотя экспериментальный материал не очень велик и не всегда является абсолютно доказательным, тем не ме — Знее можно утверждать, что все три электрокинетические явления эквивалентны и значения ^-потенциала, определенные этими тремя методами, одинаковы.
 1 ноября, 2012
1 ноября, 2012  admin
admin 
 Опубликовано в рубрике
Опубликовано в рубрике 