Для упрощения изложения будем рассматривать, в основном, плоский двойной электрический слой, хотя в коллоидных растворах и тонкопористых телах такой слой практически и не встречается. Подобное упрощение допустимо, когда толщина двойного слоя мала по сравнению с радиусом кривизны поверхности коллоидных частиц или капилляров.
|
___ ±____ ±__ +______ ±__±—— ++ +++ ++ ++++ + ++ |
|
В |
|
Ш |
|
Рис. VII, 6. Схема движения жидкости и противоионов при электроосмосе |
Кроме того, при рассмотрении двойного электрического слоя примем ряд следующих общих положений, из которых исходили все авторы теорий его строения. Двойной электрический слой состоит из ионов одного знака, относительно прочно связанных с дисперсной в случае лиозолей твердой фазой (Потенциалопреде- ляющие ионы), и эквивалентного количества противоположно за
ряженных ионов, находящихся в жидкой дисперсионной среде вблизи межфазной поверхности (противоионы). Заряд на поверхности твердой фазы в первом приближении рассматривается как поверхностный заряд, равномерно распределенный по всей поверхности. Между противоионами и свободными (не входящими в двойной электрический слой) ионами того же знака, находящимися в жидкости, существует динамическое равновесие. Дисперсионная среда представляется всегда как непрерывная фаза, влияние которой на двойной электрический слой определяется лишь ее диэлектрической проницаемостью.
При таких предпосылках отличие между теориями строения двойного электрического слоя заключается, в основном, только в различном толковании структуры слоя противоионов.
|
Рис. VII, 7. Двойной электрический (VII, 1) слой по Гельм — гольцу — Перрену и соответствующий скачок потенциала. |
|
Фо |
Теория Гельмгольца — Перрена. Согласно этой теории двойной слой представляется как бы плоским конденсатором, одна обкладка которого связана непосредственно с поверхностью твердого тела (стенкой), а другая обкладка, несущая противоположный заряд, находится в жидкости на очень малом расстоянии от первой. Потенциалов таком двойном слое, равно как и потенциал в плоском конденсаторе, очевидно, должен падать весьма круто (по прямой), а значение поверхностного заряда а будет определяться известной из физики формулой:
4лд
Где е — абсолютная диэлектрическая проницаемость среды, заполняющей пространство между обкладками конденсатора, фо — разность потенциалов между дисперсной фазой и раствором; б — расстояние между обкладками
На рис. VII, 7 дана схема строения такого двойного электрического слоя. На этом рисунке заштрихованная часть представляет твердую фазу, а незаштрихованная — раствор; положительные и отрицательные ионы, образующие двойно^ слой, обозначены соответственно через + и —; свободные ионы электролита, всегда присутствующие в жидкости, чтобы не усложнять схему, не показаны. Рис. VII, 7 иллюстрирует также падение потенциала с увеличением расстояния х от поверхности твердого тела, причем общий скачок потенциала в гаком двойном слое является в то же время и скачком потенциала между твердой фазой и раствором.
|
+ <J -6 |
Приведенная схема строения двойного электрического слоя не объясняет ряд особенностей электрокинетических явлений. В настоящее время она представляет для коллоидной химии только исторический интерес. Основным недостатком этой схемы является
то обстоятельство, что толщина двойного слоя Гельмгольца — Пер — рена очень мала и приближается к молекулярным размерам. В то же время в результате гидродинамических исследований было установлено, что место разрыва (плоскость или граница скольжения) при перемещении твердой и жидкой фаз относительно друг друга всегда находится в жидкой фазе на сравнительно большом расстоянии От межфазной границы. Толщина слоя жидкости, «прилипающего» в этих условиях к твердой поверхности, во всяком случае больше толщины двойного электрического слоя Гельмгольца — Перрена.
Если бы теория Гельмгольца — Перрена была правильной, то при оседании коллоидных частиц в жидкости или при продавли — вании жидкости через капилляр вообще не должен был бы наблюдаться эффект Дорна или потенциал протекания, а явления электрофореза и электроосмоса были бы невозможны. Однако если даже допустить, как это принималось ранее, что поверхность скольжения проходит между двумя обкладками двойного электрического слоя, то и в этом случае представления Гельмгольца — Перрена приводят к противоречию. В самом деле, при таком допущении Электрокинетический потенциал, т. е. потенциал, обнаруживаемый при электрофорезе или электроосмосе, должен был бы соответствовать разности между всеми потенциалопределяющими ионами и всеми противоионами, т. е. равняться общему скачку потенциала. Однако опыты показали, что электрокинетический потенциал не только, как правило, меньше общего скачка потенциала, но изменяется под влиянием различных факторов совсем иначе. Например, общий скачок потенциала не зависит сколько-нибудь существенным образом от индифферентных’ электролитов, ие содержащих ионов, способных достраивать, кристаллическую решетку, в то же время такие электролиты сильно влияют на электрокинетический потенциал.
Все изложенное показывает, что общий скачок потенциала и электрокинетический потенциал являются различными величинами и, следовательно, представления Гельмгольца и Перрена о плоском электрическом слое недостаточны для объяснения электрокинетических явлений.
Теория Гун — Чэпмена. Значительным шагом вперед явилась теория двойного электрического слоя с диффузным слоем проти — воионов, предложенная независимо друг от друга Гуи (1910 г.) и Чэпменом (1913 г.). Эта теория в значительной мере устранила недостатки теории Гельмгольца — Перрена. По теории Гуи — Чэпмена противоионы не могут быть сосредоточены только у межфазной поверхности и образовывать моноионный слой, а рассеяны в жидкой фазе на некотором расстоянии от границы раздела. Такая структура двойного слоя определяется, с одной стороны, электрическим полем у твердой фазы, стремящимся притянуть эквивалентное количество противоположно заряженных ионов возможно ближе к стенке, а с другой стороны, тепл^ь ш движением ионов,
вследствие которого противоионы стремятся рассеяться во всем объеме жидкой фазы.
|
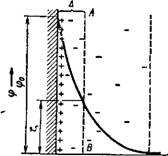
Рис. VII, 9. Двойной электрический слой по Гун — Чэпмеиу и падение в нем потенциала. |
В непосредственной близости от межфазной границы преобладает действие электрического поля. С удалением от межфазной границы сила этого поля постепенно ослабевает и проявляется все сильнее рассеивание противоионов двойного слоя в результате теплового движения, вследствие чего концентрация противоионов падает и становится равной концентрации тех же ионов, находящихся в глубине жидкой фазы. Таким образом возникает равновесный диффузный слой противоионов, связанных с твердой фазой. Понятно, что равновесие этого диффузного слоя динамическое.
|
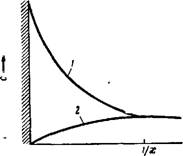
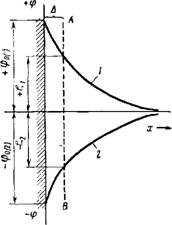
Рис. VII, 8. Зависимость концентрации С протнвоиоиов (кривая 1) и потенциалопределяющих иоиов (кривая 2) от расстояния х от плоской стеики (1 /к — толщина двойного электрического слоя). |
С другой стороны, находящиеся в жидкости ионы того же знака, что и адсорбированные стенкой потенциалопределяющие ионы, отталкиваются электрическими силами от твердой фазы и уходят в глубь раствора. Это обусловливает распределение потенциалопределяющих иоиов и противоионов в диффузной части двойного электрического слоя, что иллюстрирует рис. VII, 8.
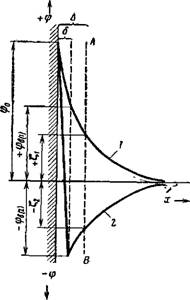
Строение двойного электрического слоя по Гуи — Чэпмену и падение потенциала в этом слое схематически изображены на рис. VII, 9.- Потенциал на этой схеме падает не по прямой, а по кривой в связи с тем, что компенсирующие заряд стенки противоионы распределены неравномерно. Падение кривой круче в тех местах, где больше компенсирующих противоионов, и, наоборот, кривая более полога там, где компенсирующих противоионов мало.
Поскольку диффузность слоя противоионов определяется тепловым разбрасыванием, то при температуре абсолютного нуля все противоионы должны были бы находиться у твердой поверхности.
Следовательно, теоретические представления Гельмгольца — Перрена оказываются частным случаем теории Гуи — Чэпмена.
Равновесное распределение ионов, которое устанавливается у твердой стенки, аналогично равновесному распределению молекул газа в атмосфере под влиянием силы тяжести с тем лишь различием, что гравитационное поле не зависит от распределения молекул, а электрическое поле в случае двойного электрического слоя само является функцией распределения заряженных ионов. Число противоионов, находящихся у заряженной поверхности твердой фазы, по мере увеличения расстояния от границы раздела по направлению внутрь раствора, уменьшается по закону распределения Больцмана, а число потенциалопределяющих ионов увеличивается согласно тому же закону. Отсюда следует, что если концентрацию положительных и отрицательных ионов в точке, потенциал которой равен фж, соответственно обозначить через с+ и с_ (в молях на единицу объема), то для расстояния х — оо
С+ = С — = Соо
А для не слишком большого расстояния х
С+ =Соо ехр (— FzqtJRT) . ^ — ^ ОО ехр (FztfxjRT)
Где с оо — концентрация электролита на бесконечно большом расстоянии от твердой фазы при фоо = 0; F—число Фарадея (96 540 Кл); г — валентность иона; R — газовая постоянная; Т—абсолютная температура.
Согласно уравнению распределения Больцмана произведение Fz<Px в экспоненциальном множителе уравнений (VII, 3) и (VII, 4) представляет собой. электрическую работу переноса одного моля соответствующего вида ионов из объема раствора (где <р = 0) до точки с потенциалом <рж.
Ясно, что при х = оо фж = фоо = 0, а при х = 0 фж = фо, т. е. на бесконечно большом расстоянии от границы раздела потенциал равен нулю, а на границе раздела — общему скачку потенциала поверхности.
Представления, развитые Гуи и Чэпменом, позволяют объяснить некоторые электрокинетические явления. Так, поскольку плоскость скольжения АВ при перемещении твердой и жидкой фаз относительно друг друга лежит в жидкости на некотором малом расстоянии А от межфазной границы, где потенциал еще не снижается до потенциала жидкой фазы (см. рис. VII, 9), то разность между ним и потенциалом внутри жидкой фазы в этом месте соответствует заряду этой части диффузного слоя. Этот потенциал и будет определять перемещение фаз при наложении электрического поля, т. е. обусловливать явления электрофореза или электроосмоса. Ясно, что электрокинетический потенциал, как его часто называют 1,-потенциал, является частью общего скачка потенциала фо. Таким образом, становится понятным, почему электро
кинетический потенциал отличен от нуля, но не равен общему скачку потенциала. Более того, схема строения двойного электрического слоя, предложенная Гуи и Чэпменом, позволяет понять, почему различные факторы влияют на оба потенциала по-разному.
Рассмотрим, например, как влияет на оба эти потенциала введение в систему индифферентного электролита. В этом случае общий скачок потенциала почти не изменяется. Совсем иначе будет обстоять дело с электрокинетическим потенциалом. С повышением концентрации вводимого электролща вследствие того, что для компенсации потенциалопределяющих ионов требуется всегда одно и то же (эквивалентное) число зарядов противоположного знака, толщина диффузного слоя уменьшается. Как принято говорить, двойной электрический слой сжимается. В результате этого меняется и распределение в нем потенциала. Будет меняться и ^-потенциал, отвечающий плоскости скольжения жидкости при электрофорезе или электроосмосе.
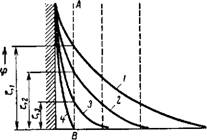
Наглядно изменение £-потен — циала при введении в систему все увеличивающихся количеств индифферентного электролита показано на рис. VII, 10. При достаточно больших концентрациях электролита диффузный слой может сжаться до моноионного слоя, и двойной электрический слой, таким образом, превратится в слой Гельмгольца — Перрена. Понятно, что поскольку этот слой будет находиться ближе к стенке, чем плоскость скольжения, £-потен — циал будет равен нулю.
Следует заметить, что в основе теории Гуи — Чэпмена лежат те же физические представления, что и в основе известной теории сильных электролитов Дебая — Гюккеля, причем, кстати заметим, первая возникла раньше второй.
Как известно, толщина ионной атмосферы 1/х по теории сильных электролитов определяется следующим уравнением:
-1 = / EkT _ / ERT _ / ERT
И Д/ 8ne2Nд £ Ctz] V **eWA £ Ctzi V Z "A
(VII, 5)
|
Рис. VII, 10. Влияние индифферентного электролита на толщину двойного электрического слоя и электро — кннетический потенциал (количество электролита увеличивается от кривой 1 к кривой 4). |
|
Х — |
Где e — абсолютная диэлектрическая проницаемость жидкости; k — постоянная Больцмана; ~Т — абсолютная температура; е — заряд электрона; NA — число Авогадро; с І — концентрация ионов различной природы; z< — валентность ионов; R — газовая постоянная; F—число Фарадея,
Уравнение VII, 5, связывающее 1/х, с, и Z„ можно представить в упрощенном виде:
VT5T
Где K — константа уравнения; — c, Zi — ионная сила раствора.
Из приведенного уравнения вытекает, что ионная атмосфера должна быть тем меньше, чем выше концентрация ионов в растворе и чем больше их валентность. Естественно^ что аналогичное соотношение соблюдается и тогда, когда ионная атмосфера образуется не вокруг иона, а вблизи границы раздела фаз. Однако только при малых потенциалах поверхности значение ^-потенциала определяется одной толщиной ионной атмосферы и только в этих условиях на нее могут одинаково влиять как заряды противоионов, так и заряды побочных ионов, присутствующих в системе. При высоких потенциалах поверхности (больше 50 мВ), как показывает теория, на снижение ^-потенциала во много раз сильнее влияет заряд противоиона, в особенности когда он велик. Физический смысл этого явления заключается в том, что сильно заряженный противоион электролита притягивается к поверхности и сильно ее экранирует. Возрастание способности противоиона снижать ^-потенциал с ростом его валентности наглядно видно нз следующих опытных данных:
Валентность противоиона IV III ГІ I
С£……………………………. 1 10-20 60-100 500-1000
«Здесь значения eg представляют собой относительную концентрацию противоиона, необходимую для снижения электрокинетического потенциала до одного. и того же значения, например 50 мВ. Как видно, этот ряд не дает каких-нибудь точных отношений. Этого, впрочем, и нельзя было ожидать, так как способность иона> сжимать двойной электрический слой зависит не только от его валентности, определяющей электрическое взаимодействие со стенкой, но и от его размера, поляризуемости, способности гидра — тироваться и т. д. Мюллер, исходя из представлений Гуи и Чэп — мена, чисто математическим путем показал^что способность противоионов понижать ^-потенциал действительно должна быстро расти с их валентностью, причем для случая плоской поверхности раздела его вычисления дали такой ряд:
Валентность противоина IV III II I С£ 1 7,5 57 540
Это достаточно хорошо согласуется с экспериментальными данными.
Рассмотрим теперь количественную сторону теории Гуи — Чэпмена.
Одним из основных исходных уравнений в этой теории является уравнение Пуассоиа, предусматривающее связь межу объемной плотностью заряда р и по-
Тенциалом ф Это уравнение имеет вид:
V<p=-4np/e (VII, 6)
Где є — абсолютная диэлектрическая проницаемость; V — сокращенное обозначение оператора Лапласа:
Уф = (<Згф /дх2) + (<Згф/ді/г) + (<32ф/<Эг*) (VII, 7)
При плоской поверхности твердой фазы потенциал изменяется только в направлении по нормали к поверхности, и производные по у и г, таким образом, равны нулю В этом частном случае зависимость потенциала от расстояния до стенки х выражается следующим простым уравнением:
D^/dx* =» — 4яр/е (VII, 8)
Очевидно, при х = ОО
Ф = 0; Dy/Dx = 0 и р = 0
А при х = 0
Ф = Фо и Dcp/Dx = — 4яа/е
Где фо — потенциал межфазной поверхности; а — заряд (поверхностная плотность электричества) той же поверхности
Объемную плотность заряда можно представить так:
P = Fe(c+-c_) (VII, 9)
Где F — число Фарадея; г — валентность ионов; с+ и с_ — концентрация положительных и отрицательных ионов, моль/л
Формула (VII, 9) пригодна, очевидно, только для бинарного симметричного электролита. В других случаях формула (VII, 9) должна иметь вид алгебраической суммы:
Р=Т. Ргісі (VII, 10)
Однако этот более сложный случай мы здесь рассматривать не будем Подставив в уравнение (VII,9) уравнения (VII,3) и (VII,4), имеем-
Р = FzcM [ехр (- Fzy/RT) — ехр (Fzq/RT)] (VII, И)
Если найденное значение р подставить в уравнение (VII, 8), можно получить:
4- — щ- ь (- — От?)] ,2>
Для того чтобы провести первое интегрирование и получить производную Dif/Dx, преобразуем полученное уравнение следующим образом:
^-^—^М-тМ-Чт?-)]
Проинтегрируем полученное выражение от 0 до <р. Учитывая, что при ф -> О ■D<F/Dx->0, имеем
О
Так как при увеличении * величина ср уменьшается! то производная Dtf/Dx ЯмеЄТ"Отри"цательй6е значение, и окончательно имеем:
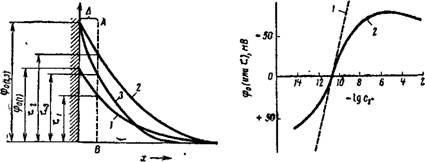
Это дифференциальное уравнение позволяет сделать ряд интересных выводов. Если электролит, концентрация’которого в растворе равна са, является индифферентным, т. е. не содержит потеициалопределяющие ионы, то и потенциал фо, равный общему скачку потенциала, не зависит от. с„. Следовательно, при изменении с0О, согласно формуле (VII, 13), может изменяться только наклон кривой ф = /(*), а значение ф0 должно оставаться постоянным. На рис. VII, 10 лриведеио несколько кривых ф = f(x), отвечающих одному и тому же значению фо, ио при разных сдля которых D<F/Dx, в соответствии с уравнением (VII, 13), возрастает от кривой 1 к кривым 2, 3, 4. Так как плоскость скольжения на рис. VII, 10 соответствует линии АВ, то понятно, что начальный электро — ■кинетический потенциал Si с возрастанием концентрации электролита будет уменьшаться, принимая значения £г> ?з и т. д. При валентности противоиона, большей единицы, производная D(F/Dx, учитывая уравнение (VII, 13), с возрастанием концентрации должна увеличиваться еще сильнее, т е. электрокииетиче — — ский потенциал будет падать еще более резко
Таким образом, теория Гуи — Чэпмена хорошо объясняет падение £-потеи — •циала при увеличении концентрации противоиона и возрастании его валеитиости.
|
Еде |
При. малых Фо и. соответственно при значениях Fztp0/(2RT) <С 1 можно воспользоваться приближением еа = 1 +а и е~а= 1 —а, что дает еа — е~а = 2а. Тогда вместо уравнения (VII, 13) получим приближенное уравнение:
Гіф / 8NR Тсх Fz(F _ / 8NF2Z2Cx
47 =-Л/—г——————— WT^-У ERT 4>=->"P
/ 8nF2z2cx _ / 8яE2z2MAcx
Интегрируя уравнение (VII, 14) и учитывая, что при * — _0 _<р = jjto,. получаем:
|
Или |
<р = фоЄ-** (VII, 15)
Уравнение (VII, 15) показывает, что потенциал уменьшается в е — 2,72 раз на расстояний порядка 1/х*.
Уравнение (VII, 13) позволяет установить соотношение между плотностью поверхностного заряда о на межфазной границе и потенциалом поверхности фо. Из условия электронейтральности двойного электрического слоя следует, что поверхностный заряд по абсолютному значению равен общему объемному заряду в растворе, т. е.
Оо
(VII, 16>
О
С помощью уравнения Пуассона (VII, 8) это уравнение можно проинтегрировать следующим образом:
J 4я Dx2 4я V Dx Jx= О ‘
О
Заменяя Dif/Dx найденным для этой производной значением из уравнения (VII, 13), получаем:
‘ " V-тг*- Ь Шг) ~ "" (" "гіг)] <™.»>
Пользуясь упрощением, аналогичным тому, которое было применено при выводе формулы (VII, 14), из уравнения (VII, 18) в случае малых значений фо и Fzya/ZRT можно получить следующее приближенное выражение:"
|
V |
ERTCn Ґ2фо Є / вяЯ^Сд, ех 10.
—2S——— = SRT • 4,0 =Ж’фо № 19>
Где
8Ne*Z2NAc ERT V вкТ
В этом случае заряд и потенциал на границе раздела пропорциональны друг другу и двойной электрический слой ведет себя как плоский конденсатор, расстояние между пластинами которого равно 1/х « б. То, что расстояние между обкладками конденсатора, эквивалентное двойному слою, равно примерно 1/х, оправдывает обычный способ выражения: «толщина двойного электрического слоя равна 1/х».
Важным свойством двойного электрического слоя, которое легко охарактеризовать количественно, является его дифференциальная и интегральная емкость:
<Зс/дфо и с/фо (VII, 20)
Для небольших потенциалов дифференциальная и интегральная емкости равны одной и той же величине С, которую можно вычислить по уравнению:
С = о/фо = ех/(4я) (VII, 21)
Для более высоких потенциалов емкость двойного электрического слоя становится больше этой величины.
При комнатной температуре и г = 1 значение к равно приблизительно 3-Ю7 V7 (где с — концентрация электролита, моль/л) Отсюда в 1 н водном растворе электролита с одновалентными катионом и анионом вычисленная емкость двойного электрического слои равна 3-107-80/4 = 200 мкФ/см2 Емкости, определенные экспериментально, равны всего одной десятой этого значения
Несостоятельность теории Гуи — Чэпмена может быть показана и другим путем Если раствор электролита не очень разбавлен (например, 0,1 н) и потенциал у стенки высок (например, 200 мВ), то для того, чтобы теоретическое И экспериментально найденное значения емкости совпадали, концентрация про — тивоиона около стенки должна быть равна 300 н, что совершенно невозможно^ Причина расхождения экспериментально и теоретически найденных значений емкости двойного электрического слоя заключается в том, что теория Гун — Чэпмена не принимает во внимание размера ионов, рассматривая их как точечные заряды, которые могут сколь угодно близко подойти к стенке, что и обусловливает более высокие значения расчетных величин
Другой недостаток теории Гуи — Чэпмена заключается в том, что она не объясняет так называемого явления перезарядки — перемены знака электрокинетического потенциала при введении в систему электролита с многовалентным ионом, заряд которого противоположен по знаку заряду дисперсной фазы.
Далее теория Гуи—Чэпмена не объясняет различного действия разных по природе противоионов одной и той же валентности на двойной электрический слой. Согласно этой теории введение эквивалентного количества разных противоионов одинаковой валентности должно сжимать двойной электрический слой и понижать ^-потенциал в одинаковой степени. Однако опыт показывает, что это не так. Эффективность действия ионов одной и той же валентности на двойной электрический слой возрастает с увеличением радиуса иона.
Наконец, теория Гуи — Чэпмена, относительно хорошо прило — жимая в случае достаточно разбавленных коллоидных растворов, оказывается неприемлемой для более концентрированных.
Все эти затруднения в значительной мере преодолены в теории строения двойного электрического слоя, предложенной Штерном
Теория Штерна. В 1924 г. Штерн предложил схему строения двойного электрического слоя, в которой он объединил схемы Гельмгольца — Перрена и Гуи — Чэпмена. Разрабатывая теорию двойного электрического слоя, Штерн исходил из двух предпосылок. Во-первых, он принял, что ионы имеют конечные^ вполне определенные размеры и, следовательно, центры ионов не могут находиться к поверхности твердой фазы ближе, чем на расстоянии ионного радиуса. Во-вторых, Штерн учел специфическое, не электрическое взаимодействие ионов с поверхностью твердой фазы. Это взаимодействие обусловлено наличием на некотором малом расстоянии от поверхности поля молекулярных (адсорбционных) сил. Как будет показано при обсуждении причин устойчивости и коагуляции коллоидных систем, молекулярные силы, действующие между телами, состоящими из множества молекул, вследствие своей аддитивности являются относительно дальнодействующими.
Однако в отличие от электрических сил их действие быстро уменьшается с расстоянием, и поэтому их действие в данном случае следует учитывать только у самой поверхности твердого тела на расстоянии порядка нескольких ангстрем.
Согласно Штерну, первый слой или даже несколько первых слоев противоионов притягиваются к стенке под влиянием как электростатических, так и адсорбционных сил. В результате этого часть противоионов удерживается поверхностью на очень близком расстоянии, порядка 1—2 молекул, образуя плоский конденсатор толщиной б, предусмотренный теорией Гельмгольца — Перрена. Этот слой, в котором, естественно, наблюдается резкое — падение электрического потенциала, одни авторы называют гельмгольцевским, другие — Штерновским, третьи — адсорбционным слоем. Остальные противоионы, нужные для компенсации потенциалопре — деляющих ионов, в результате теплового разбрасывания образуют диффузную часть двойного слоя, в которой они распределены согласно тем же законам, что и в диффузном слое Гуи — Чэпмена. Эту часть двойного слоя, в которой потенциал падает относительно постепенно, иногда называют слоем Гуи. Схема двойного электрического слоя по Штерну и падение в нем электрического потенциала показаны на рис. VII, II.
Из схемы можно видеть, что полное падение потенциала фо слагается из падения потенциала ф6 в диффузной части двойного слоя и разности потенциалов (ф0 — ф6) между обкладками конденсатора. Место границы скольжения в таком слое остается до сих пор неясным. Некоторые авторы принимают, что она совпадает с границей между слоем Гельмгольца и слоем Гуи. Однако в общем случае ее можно представить себе находящейся в слое Гуи, как это изображено на рис. VII, 11 (граница скольжения обозначена пунктирной линией АВ). Таким образом, потенциал на границе слоя Гельмгольца и слоя Гуи не обязательно должен быть равен ^-потенциалу.
Понятно, что с введением электролитов в систему диффузный слой будет сжиматься и все большее и большее число противоионов будет попадать в адсорбционный слсш. Двойной электрический слой, согласно-взрдяДам Штерна, при этом все больше приближается к слою, предусмотренному в теории Гельмгольца — Перрена, а ^-потенциал уменьшается, постепенцо-лцшйгшжаясь к нулю При разбавлении системы, наоборот, диффузный слой расширяется и ^-потенциал возрастает.
На распределение ионов в двойном электрическом слое по теории Штерна сильно влияет природа противоионов. Если противоионы обладают различной валентностью, то толщина диффузного слоя и число противоионов в адсорбционном слое определяются, главным образом, валентностью ионов и, следовательно, обусловливаются электростатическими силами. Понятно, диффузный слой тем тоньше и ^-потенциал тем ниже, чем больше валентность йро — тивоионов. При этом надо принимать во внимание те же соображения, что и при объяснении влияния валентности противоиона на ^-потенциал по теории Гуи — Чэпмена.
Если противоионы имеют одинаковую валентность, толщина двойного электрического слоя и число противоионов в диффузном слое определяются специфической адсорбционной способностью ионов, обусловленной, как показано в гл. VI, их поляризуемостью и гидратацией. Эти свойства ионов определяются их истинным радиусом или, что то же, положением соответствующих элементов в таблице Д. И. Менделеева.
Большая поляризуемость иона, конечно, должна способствовать уменьшению толщины двойного электрического слоя, поскольку при этом возникают дополнительные адсорбционные силы между твердой фазой и индуцированным диполем и, кроме того, ион может ближе подойти к поверхности. Так как деформируемость иона увеличивается с его размерами и поскольку радиусы анионов вообще значительно больше радиусов катионов, поляризуемость анионов обычно больше, чем катионов:
|
Катион |
AlO24, см3 |
Анион |
AlO24, cm’ |
|
Li* |
0,03 |
F" |
0,96 |
|
Na+ |
0,19 |
Ci- |
3,60 |
|
К+ |
‘0,89 |
Br" |
5,00 |
|
Rb+ |
1,50 |
R |
7,60 |
|
Cs+ |
2,60 |
В этом, между прочим, кроется объяснение того, почему отрицательный заряд поверхности встречается в природе гораздо чаще, чем положительный.
Гидратация ионов, как известно, уменьшается с увеличением истинного радиуса ионов. Снижение гидратации ионов должно способствовать сжатию двойного электрического слоя, так как гидрат — ная оболочка уменьшает электростатическое взаимодействие между противоионами и поверхностью твердой фазы.
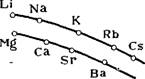
Из всего приведенного становится понятным, почему способность сжимать двойной электрический слой и уменьшать ^-потенциал возрастает в ряду катионов от Li+ к Cs+, а в ряду анионов от F — к I". На рис. VII, 12 приведена найденная Енни и Рейтемейе — ром зависимость ^-потенциала отрицательно заряженных частиц водной суспензии глины, насыщенной различными одно — и двухвалентными противоионами, от размера ионов. Как можно видеть,
Характер зависимости ^-потенциала от радиуса двухвалентных катионов такой же, что и для одновалентных катионов.
Рассмотрим теперь представления Штерна, с количественной стороны.
По абсолютной величине заряд о на твердой поверхности, согласно теории Штерна, равен сумме заряда ионов, находящихся в адсорбционном слое ai, и заряда диффузной части двойного слоя 02:
|
|
|
Г_=Г„ |
|
Рис. VII, 12. Зависимость £-по — тенциала отрицательно заряженных частиц глины от радиуса противоионов г. |
0 = 01+02 (VII, 22>
Для вычисления 01 Штерн использовал метод, аналогичный тому, который применяется для вывода изотермы адсорбции Ленгмюра. Для симметричного электролита (у которого оба иона имеют один и тот же заряд) Штерн получил следующие уравнения, характеризующие число адсорбированных единицей поверхности молей ионов различного знака:
I
Г+=ГЫ
L + l/Cooexp[(e+ + Fz<p6)//?r] (VII, 23)
______________ Г_____________
1 + 1 /Соі ехр [(0_ — Fz%)IRT]
(VII, 24)
Где 9+ и 0- — специфические адсорбционные потенциалы для положительных и отрицательных ионов.
В уравнениях (VII, 23) и (VII, 24) числитель экспоненты представляет общий адсорбционный потенциал ионов, т. е. работу
Переноса одного моля ионов из объема раствора на поверхность адсорбента. Эта сложная величина, представляющая алгебраическую сумму специфического адсорбционного потенциала 6+ или 8- и электрического адсорбционного потенциала Fzcpj. Для положительных иоиов общий адсорбционный потенциал, очевидно, будет 9+ + Fztpj, для отрицательных он равен 0- — Fz(pj.
Заряд адсорбционного слоя 0i представляет собой разность отрицательных и положительных зарядов, приходящихся на единицу адсорбционной поверхности. Тогда
1
I + 1/ею ехр [(9+ + Fz<p0)/RT]
________________ 1_____________
|
С = Fz (Г+ — Г—) = FzTK |
|
(VII, 25) |
1 — Н/Сооехр [(8_-Ларв)//гГ]
На практике очень часто достаточно принимать в расчет только одно из слагаемых в уравнении (VII, 25), так как или положительные, или отрицательные ионы полностью вытесняются из молекулярного конденсатора. Другое упрощение сводится к тому, что единицу в знаменателе обоих уравнений можно отбросить, если концентрация электролита не слишком высока.
Заряд диффузного слоя 02 непосредственно «связан с потенциалом в этом слое фб и вычисляется согласно теории Гуи — Чэпмена по уравнению (VII, 18) (т. е. в этом случае действие адсорбционных сил не учитывается):
Подставляя уравнения (VII, 25) и (VII, 26) в уравнение (VII, 22), получим:" ( 1
О ^гГ„акс I j jCoo ex(j — г і іфj
1 + 1/с„ ехр [(9_ — Fz<P6)/2RT] ) +
Так как значение первого члена выражения в фигурных скобках в правой части равенства меняется с концентрацией сильнее, чем значение второго, то, очевидно, при разбавлении раствора уменьшается быстрее, чем о2, и структура слоя приближается к модели Гуи — Чэпмеиа, при увеличении же концентрации структура двойного электрического слоя приближается к модели Гельмгольца Таким образом, анализ уравнения (VII, 27) приводит к тем же выводам, к которым мы пришли ранее иа основании общих положений.
Первый член суммы в правой части уравнения а (см. VII, 27) представляет интерес еще и потому, что даже тогда, когда 0+ и 9_ равны нулю, т. е. при отсутствии специфической адсорбции, величина at все же ие равна нулю Это ■ значит, что противоиоиы, даже если оии ие адсорбируются специфически, могут втягиваться в адсорбционный слой под действием электростатических сил.
Емкость полного двойного слоя С определяется как емкость двух последовательно расположенных конденсаторов по известной формуле:
Си • Сд (VII>
С м + Сд
Где Си—емкость молекулярного конденсатора; Сд— емкость диффузного слоя. Емкость молекулярного слоя Си равна отношению заряда стенки а к разности потенциалов <р0 — щ:
СМ = <*!(%-%) (VII, 29)
Штерн принимал емкость молекулярного конденсатора постоянной. Однако эта емкость, безусловно, должна зависеть от специфических свойств иоиов, находящихся в адсорбционном слое. Так как величина С„ почти постоянна, а величина Сд сильно зависит от концентрации электролита, характер падения потенциала в двойном электрическом слое также зависит от количества находящегося в системе электролита. Таким образом, если даже потенциал <р0 является постоянным, то фй, значение которого определяется состоянием диффузного слоя, снижается с уменьшением 1/я.
Если емкость одного из двух конденсаторов значительно больше емкости другого, то полная емкость практически равна меньшей составляющей. Так, в разбавленных растворах С я» Сд, а в концентрированных С « С„.
Значения емкости двойного электрического слоя, вычисленные по теории Штерна с учетом радиусов ионов, оказались близкими к экспериментально найденным, и, таким образом, эта теория преодолела один из недостатков, присущий теории Гуи — Чэпмена. Далее, в отличие от теории Гуи — Чэпмена, теория Штерна может Объяснить причину изменения знака электрокинетического потенциала при введении в систему многовалентных ионов, заряд которых противоположен по знаку заряду дисперсной фазы. Такие мно: говалентные ионы втягиваются в адсорбционный слой как из-за сильных электростатических взаимодействий, так и из-за большой адсорбируемости, связанной с поляризуемостью таких ионов. Ионы
могут адсорбироваться^^в^таком количестве, что не только нейтрализуют заряд твердой поверхности, но и перезаряжают частицу. В результате, как это можно видеть из схемы рис. VII, 13, характер падения потенциала в двойном электрическом слое изменится коренным образом, а ф6- и ^-потенциалы, имевшие ранее тот же знак, что и ф-потенциал (на схеме Ф6і и меняют знак на обратный (на схеме ф62 и £2)- При этом, конечно, потенциал фо остается постоянным, так как чужеродные ноны не способны достраивать кристаллическую решетку твердой фазы. Таким образом, создается положение, когда Фо- и ^-потенциалы будут иметь различные знаки. ПоняРгао, что дальнейшее повышение концентрации электртошта в "системе долждо-~при — водить к сжатию-диффузного слоя и падению ^-потенциала.
Для перезарядки частиц, имеющих отрицательный ^-потенциал, особенно часто применяют многовалентные ионы алюминия и тория. Впрочем, перезарядку способны вызывать и одновалентные ионы, если они обладают * большим адсорбционным потенциалом. Сюда относятся ионы многих алкалоидов, например стрихнина и хинина, и основных красителей (кристаллический фиолетовый, метиленовый голубой и др.). Это объясняется тем, что такие крупные ионы не только способны поляризоваться, но и являются постоянными диполями. ч
|
Рис. VII, 13. Изменение падения потенциала двойного электрического слоя при перезарядке с помощью сильно адсорбирующихся ионов: 1— падение потенциала до перезарядки; 2— падение потенциала после переза Рядки. |
Из изложенного выше видно, что теория Штерна соответствует результатам экспериментальных наблюдений лучше, чем теория Гуи — Чэпмена. Благодаря уточнению роли размера ионов и введения представления об адсорбционном потенциале, она может объяснить ряд специфических особенностей действия тех или иных электролитов на двойной электрический слой и электрокинетический потенциал. Однако необходимо указать, что и эта теория не является совершенной, поскольку она исходит из ряда допущений и в ней имеется много неопределенностей, например, допущение о независимости адсорбционного потенциала от концентрации, что едва ли вероятно. Следует также заметить, что представления р плоскости скольжения в двойном электрическом слое весьма условны. По существу, плоскости скольжения так, как ее представ
лял Штерн, очевидно, нет, а имеет место скольжение жидкости от межфазной поверхности в глубь раствора, начинающееся на определенном расстоянии от поверхности твердой фазы. Таким образом, значение ^-потенциала, весьма важной характеристики всякой коллоидной системы, определяется при электрокинетических явлениях не только характером падения потенциала в двойном электрическом слое, но и характером движения жидкости
Вблизи твердой пбверхности, зависящим от ее реологических свойств.
В дальнейшем был проведен ряд исследований с целью уточнить предположенное Штерном строение двойного электрического слоя. Из этих исследований наибольшее значение имеет работа Грехема, согласно которой слой Гельм — гольца состоит из внедіней н внутренней частей. Во внешней части находятся гидратированные противоионы, которые удерживаются у мегкфазной поверхности электростатическими силами. Во внутренней части находятся хемосорбирован — ные твердой поверхностью ионы, одноименно заряженные с твердой фазой и с частично разрушенными гидратными оболочками.
Строение двойного электрического слоя у сферических частиц. Для сферических частиц при сравнительно небольших значеннях потенциала фо приближенное выражение для падения потенциала с расстоянием было дано Дебаем и Гюккелем:
Ф = (ф0г/а) ехр [— х(а — г)] (VII, 30)
Где г —радиус частицы; а — расстояние от ее центра. Заряд частицы Q прн этом зависит от потенциала ф0 следующим образом:
Q — re(l+w)(p0 (VII, 31)
Нахождение подобных зависимостей для больших значений потенциала ф0 является пока весьма сложной задачей в связи с возникающими при этом принципиальными н математическими трудностями. Однако имеются специальные таблицы, которые составили J1W, Овербек и Вирзема, позволяющие находить связь между зарядом и потенциалом сферических частиц.
Строение двойного электрического слон у частиц с постоянным дипольным моментом. Н. А. Толстой с сотр. показали, что существуют коллоидные частицы с электрической дипольной структурой, образующиеся вследствие самопроизвольной униполярной ориентации адсорбированных на их поверхности диполей дисперсионной среды (например, Н20, ОН" н т. д) или вследствие ориентации полярных групп самого вещества частиц. Подобные частицы, как показали различные электрооптические методы исследования, обладают жестким большим электрическим моментом (тысячи и миллионы дебаев). Так, перманентная дипольная структура обнаружена у пятиокнсн ванадия, у частиц суспензий глины, гуминовых золей, суспензий ряда красителей н некоторых бактерий и вирусов. Можно с достаточной уверенностью сказать, что подобные дипольные структуры, привлекшие в последнее время особое внимание исследователей, широко распространены в коллоидных и биологических системах.
Вследствие наличия постоянных диполей частицы могут взаимодействовать друг с другом и образовывать в золе сложные структуры.
Электрическую структуру коллоидной частицы, имеющую постоянный диполь, можно в первом приближении представить как взаимодействие двойного электрического слоя Гуи — Чэпмена и дипольной структуры (рис. VII, 14).
Аналогичные взаимодействия. наблюдаются и у магнитных дисперсных частиц
3. ВЛИЯНИЕ РАЗЛИЧНЫХ ФАКТОРОВ НА ЭЛЕКТРОКИНЕТИЧЕСКИЙ ПОТЕНЦИАЛ
Поскольку ^-потенциал в некоторых случаях является величиной, характеризующей устойчивость коллоидной системы, весьма важно рассмотреть влияние на него таких факторов, как введение в систему электролитов, изменение рН, концентрации раствора, температуры и т. д.
Влияние индифферентных электролитов. Рассмотрение влияния различных факторов на ^-потенциал целесообразно начать с наиболее простого и практически чрезвычайно важного случая — введения в систему индиффершхных электролитов, т. е. электролихов, не имеющих ионов, способных’ достраивать кристаллическую решетку коллоидной частицЬі. Следует указать, что именно введением индифферентных элёктр’олитов на практике чаще всего пользуются для коагуляции коллоидных систем.
Как уже было показано, индифферентные электролиты не могут сколько-цибудь существенно изменить общий скачок потенциала коллоидных частиц, а электрокинетический потенциал такие электролиты в общем случае снижают в результате увеличения концентрации противоионов и сжатия двойного электрического слоя.
При введении индифферентных электролитов следует различать два случая: 1) в систему вводится электролит, один из ионов которого одинаков с противоионами, 2) в систему вводится электролит, не имеющий общих ионов с электролитом — стабилизатором.
Первый случай рассмотрен при обсуждении теорий Гуи — мена и Штерна. Очевидно, по мере увеличения содержания в системе такого электролита толщина двойного электрического слоя стремится стать равной толщине адсорбционного слоя за счет сжатия диффузного слоя. В результате ^-потенциал понижается, пока не станет равным нулю, что будет отвечать так называемому Изоэлектрическому состоянию систему,.
Второй случай, когда в систему вводится электролит, не содержащий обоих ионов с электролитом — стабилизатором, отличается от первого только тем, что здесь имеет место явление обмена противоионов коллоидной частицы на эквивалентное число одинаковых по знаку ионов введенного электролита. Наиболее простой обмен иоеов происходит, когда на поверхности твердой фазы имеется двойной электрической слой типа Гуи — Чэпмена, т. е. когда можно пренебречь специфическим адсорбционным потенциалом ионов. Очевидно, при этом обмен будет определяться только валентностью ионов. Например, если отрицательно заряженная дисперсная фаза находится в растворе, содержащем два
вида одновалентных катионов, то отношение концентраций этих ионов в любой точке двойного сдоя должно быть тем же, что и их отношение в глубине раствора. Ионной обмен, очевидно, будет подчиняться закономерности, аналогичной уравнению Б. П. Никольского (VI, 6):
|
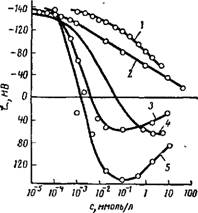
Рис. VII, 15. Влияние на ^-потенциал межфазной поверхности стекла следующих электролитов: 1 — КС1; 2—Ca(NO,),; 3—Al<NOs)j; 4—Кристаллический фиолетовой; 5—Th(NOi)«. |
Gi/g2 = ft(c./c2) (VII,32)
Где gi и g2 — концентрация ионов 1 Vi 2 электролита в двойном слое; С] и с2 — концентрация этих ионов в растворе.
Если валентность противоионов неодинакова, то равновесие при обмене значительно смещено в сторону катиона с более высокой валентностью, который в большем количестве накапливается в местах с отрицательным потенциалом. ‘
При наличии специфической адсорбции ионов ионный обмен сильно усложняется. При этом ИонЬї одной и той же валентности по своей способности переходить в двойной электрический слой располагаются в те же ряды, которые уже были приведены при обсуждении зависимости толщины двойного электрического слоя от природы образующих его ионов.
Предложено большое число уравнений для количественного описания ионного обмена, учитывающих специфическую адсорбцию ионов. Наиболее общим из таких уравнений, приложимым только к обмену иоиов одинаковой валентности, является следующее:
Ві/А-/(ві/с,) (VII, 33)
В этом уравнении коэффициент F является величиной, обусловленной различием специфических адсорбционных потенциалов 6i и 62 обоих иоиов:
F-exp(ii^L] (VII, 34)
При очень большом адсорбционном потенциале ионы, заряд которых по знаку противоположен заряду дисперсной фазы, могут вызвать перезарядку коллоидных частиц. Это явление было рассмотрено при изложении теории Штерна.
На рис. VII, 15 в качестве примера приведены кривые, характеризующие изменение ^-потенциала стекла при введении в коллоидный раствор различных электролитов [14] (данные заимство-,
ваны из работы Ратджерса и Де Смета). Как можно видеть, электролиты с одно — и двухвалентными катионами (кривые 1, 2) Только понижают ^-потенциал отрицательно заряженной стеклянной поверхности, в то время как электролиты с трех — и четырехвалентным катионом вызывают перезарядку (кривые 3, 4, 5).
Рассматривая влияние индифферентных электролитов, мы принимали, что на электрокинетический потенциал оказывают влияние ионы, заряд которых противоположен по знаку заряду коллоидной частицы и одинаков с зарядом противо* ионов Возникает вопрос, могут ли влиять на ^-потенциал ионы вводимого индифферентного электролита, заряженные одноименно с коллоидной частицей (так называемые сопутствующие или побочные ноны). На этот вопрос исследователя отвечают по-разному, но во всяком случае, если эти ионы и влияют на электрокинетический потенциал, то незначительно. К этому вопросу мы возвратимся в гл. IX.
|
19^ |
•100 I
|
V
Рис. VII, 16, Влияние иеиндиффе — рентиого электролита иа фо — и Потенциалы: 1—кривая падения потенциала в двойном электрическом слое до введения электролита; 2—то же после введения неиндиффе — реитиого электролита; 3 —то же после введения значительного количества иенидиф — ферентиого электролита. ♦ JOflL Рис. VII, 17. Зависимость потенциала фо (кривая 1) и ^-потенциала (криваи 2) частиц золя Agl от логарифма концентрации иодид-иоиов в растворе. |
Влияние неиндифферентных электролитов. Влияние электролита, один из ионов которого способен достраивать кристаллическую решетку дисперсной фазы, заключается в том, что потенциал — определяющий ион этого электролита может повышать потенциал TOo, а находящийся с ним в паре ион, одноименный с зарядом противоиона, способен сжимать двойной электрический слой. При малых концентрациях неиндифферентного электролита проявляется, в основном, первая тенденция, связанная с поверхностным действием иона, способного достраивать кристаллическую решетку. При больших концентрациях, когда достройка кристаллической решетки завершена, превалирует вторая тенденция. Поэтому при введении в систему все возрастающих количеств неиндифферентного электролита ^-потенциал сначала возрастает, а потом падает, проходя через максимум, Это видно из схемы, представленной на Рис. VII, 16.
7 Зак. 664
На рис. VII, 17 приведены данные Трельстра и Кройта, характеризующие изменение фо — и ^-потенциалов частиц золя иодида серебра в зависимости от логарифма концентрации иодид-ионов (lgfj-) в растворе. Характер изменения обоих потенциалов с изменением концентрации потенциал — определяющих ионов вполне согласуется со всем сказанным выше.
При введении неиндифферентного электролита возможна и перезарядка коллоидных частиц. Сущность такой перезарядки поясним на следующем примере. Рассмотрим, что будет происходить при введении в золь иодида серебра, стабилизованный нитратом серебра, раствора иодида калия. До введения электролита потенциалопределяю — щим ионом в золе, очевидно, будет ион Ag+, а противоионом — ион NO3. Частицы такого золя заряжены положительно. После введения в систему избытка иодида калия потен — циалопределяющим ионом станет ион 1~, а противоионом — ион К+- Сами же частицы золя приобретут отрицательный заряд. Кроме того, нитрат серебра, содержащийся в дисперсионной среде, вступит в реакцию с введенным иодидом калия, в результате чёго в системе образуется некоторое дополнительное количество отрицательно заряженной дисперсной фазы. Этот случай перезарядки отличается от уже рассмотренного случая перезарядки с помощью чужеродных ионов тем, что здесь происходит изменение не только І-, но и фо-потенциала. Схема, поясняющая перезарядку дисперсной фазы с помощью неиндифферентного электролита, показана на рис. VII, 18.
Влияние рН среды. Значение рН дисперсионной среды может сильно сказываться на ^-потенциале коллоидных частиц, так как водородные и гйдроксильные ионы обладают высокой способностью адсорбироваться; первые — благодаря" малому радиусу, что позволяет им близко подходить к поверхности твердой фазы; вторые — из-за большого дипольного момента.
|
F |
|
Рис. VII, 18. Изменение ф0- и ^-потенциалов при перезарядке С помощью неиндифферентного Электролита: 1—падение потенциалов до перезарядки; 2—падение нотеициалов после перезарядки. |
|
І |
Особое значение приобретает влияние рН для лизолей, у котрых дисперсная фаза является амфотерным соединением, например золи А1(ОН)з, Fe(OH)3, Sn(OH)4, Th(OH)4. У этих золей с изменением рН дисперсионной среды может происходить перезарядка частиц, вследствие изменения характера ионизации ве
щества дисперсной фазы. Рассмотрим перезарядку этого типа на примере золя гидроокиси алюминия.
В не слишком кислой среде ионизация молекул А1(ОН)3> находящихся на поверхности коллоидных частиц, идет следующим образом:
А1(ОН)3 А1(ОН)+ + ОН-
Гидроокись ведет себя здесь как основание, так как избыток водородных иоиов подавляет ионизацию по кислотному типу. В результате потеициалопределяющим ионом в этом случае является нон АЦОН)*, а пр. отивоионом — ОН". Коллоидная частица при этом будет заряжена положительно. В средах с более низким рН образуются ионы А134:
A’i(OH)^" + ОН — < ‘ А13+ -+- ЗОН-
Сначала это приведет к большему увеличению общего положительного заряда поверхности, а затем гидроокись алюминия растворится в кислоте и, следовательно, коллоидный раствор перейдет в истинный.
В щелочной среде ионизация по основному типу невозможна из-за избытка гидроксильных ионов. В щелочной среде гидроокись алюминия ведет себя как кислота, и ионизация А1(ОН)3 идет по следующей схеме:
А1(ОН)3 А1(0Н)20" + Н+
В результате этого потеициалопределяющим ионом уже будет ион А1(0Н)20~, а противоионом — Н Коллоидная частица окажется заряженной отрицательно. В средах с более высоким рН происходит образование иона AlOg по схеме:
А1(0Н)20" + Н+ ^ АЮ2- + Н+ + Н2О
При еще большей концентрации гидроксильных ионов гидроокись алюминия растворится в растворе щелочи с образованием алюмината и коллоидный раствор также перейдет в истинный.
Естественно, что при изменении потенциала ф0 у коллоидных частиц будет изменяться и С-потенциал. В кислой среде ^-потенциал, как и ф0-потенциал, имеет положительный знак, в щелочной среде — отрицательный. Очевидно также, что должно существовать такое значение рН, при котором ^-потенциал равен нулю и система окажется в так называемом изоэлектрическом состоянии. При этом состоянии число положительных и отрицательных зарядов на поверхности одинаково.
Приведенный пример перезарядки дисперсной фазы отличается от ранее рассмотренного случая перемены знака С-потенциала при введении неиндифферентного электролита только тем, что ион, определяющий потенциал после перезарядки, не вводится в систему, а образуется из вещества самой дисперсной фазы в результате изменения характера ионизации.
|
7* |
Влияние концентрации коллоидной системы. Исходя из самых общих представлений, можно предполагать, что при разбавлении всякой коллоидной системы g-потенциал должен возрастать, так как толщина двойного электрического слоя увеличивается в результате уменьшения концентрации противоионов в растворе. Вместе с тем при разбавлении может наблюдаться десорТэция потен — циалопределяющего иона с поверхности дисперсной фазы, что должно приводить к падению фо-потенциала и соответственно ^поТенциала. Концентрирование коллоидной системы обуславливает, конечно, прямо противоположное действие. В каком направлении в итоге изменяется ^-потенциал при измеиедии концентрации коллоидной системы, очевидно, определяется тем, влияние какого из
двух факторов — утолщения (сжатия) двойного электрического слоя или десорбции (адсорбции) потенциалопределяющих ионов — в данном конкретном случае окажется сильнее.
Влияние температуры. Аналогично концентрации на ^-потенциал действует и температура. С повышением температуры ^-потенциал должен расти вследствие возрастания интенсивности теплового движения противоионов н увеЛВДашвж ЗЯМШЩЫ двашшга электрического слоя. Однако одновременно может возрастать и десорбция потенциалопределяющих ионов, и при этом фа- и ^-потенциалы уменьшаются. При понижении температуры должна наблюдаться обратная зависимость. Вопрос о том, как будет изменяться ^-потенциал с изменением температуры, очевидно; должен решаться отдельно для каждой коллоидной системы с учетом ее индивидуальных особенностей.
Понятно, что вышеприведенные рассуждения прнложимы только к тому случаю, когда разбавление (нагревание) или концентрирование (охлаждение) системы существенно не влияют на растворимость стабилизующего электролита и на переход его из молекулярной в ионизированную форму.
Следует отметить, что, к сожалению, экспериментальных данных о влиянии на ^-потенциал частиц различных лиозолей как концентрации дисперсной фазы, так и температуры очень мало.
Влияние природы дисперсионной среды. Как отмечалось в наЧале этой главы, электрокинетические явлення, а следовательно, и наличие двойного электрического слоя на межфазной границе характерны для систем с, полярными дисперсионными средами. Большое число проведенных исследований* показало, что ^-потенциал дисперсной фазы тем больше, чем больше полярность растворителя. В табл. VII, 1 приведены результаты определения ско-
|
Таблица VII. 1. Скорость электроосмотического переноса различных жидкостей в стеклянных капиллярах
|
Ростей электроосмотического переноса некоторых чистых жидкостей в стеклянных капиллярах, полученные в опытах Файербра — зера и Балкина. Как следует из данных таблицы, чем больше полярность жидкости, характеризуемая ее диэлектрической проницаемостью и дипольным моментом молекулы, тем больше скорость электроосмотического переноса.
Влияние неравновесных электроповерхностных сил. Выше были рассмотрены равновесные поверхностные силы, действующие у межфазной границы и способные препятствовать сближению двух одноименно заряженных частиц. В последние годы Б. В. Дерягин и С. С. Духин проанализировали действие электропо — верхностиых сил в системах, в которых имеют место нарушения термодинамического равновесия. Они установили, что деформация двойного электрического слоя, вызванная внешним электрическим полем или конвективным движением жидкости, приводит к образованию такого электрического поля, радиус действия которого часто на несколько порядков превосходит радиус действия не- деформироваииого слоя в тех же условиях.
Вопросу поляризации двойного электрического слоя посвящены также работы Овербека, Буутса, Ньюмеиа и других исследователей. В этих работа авторы пришли к выводу, что осмотическим влиянием можно пренебречь при малом значении С-потеициала (£ < 25 мВ) или же при очень малой толщине двойного электрического слоя.
Теория неравновесных поверхностных сил диффузионной природы, развитая Б В. Дерягииым и С. С. Духииым, имеет существенное значение при рассмотрении закономерностей электрокииетических явлений и взаимодействия поляризованных частиц. Учет диффузии и поляризации двойного слоя позволил Б В. Де — рягииу и С. С. Духину предсказать новое явление, родственное электрофорезу,— Диффузиофорез, заключающееся в движении дисперсных частиц прн отсутствии внешного электрического поля под влиянием только перепада концентрации ионов
Роль электроповерхиостных неравновесных сил в различных процессах, вероятно, весьма значительна. Деформация двойного электрического слоя может происходить не только под действием внешнего электрического поля (этот случай будет рассмотрен в разд. 5 настоящей главы), ио и при действии конвективных потоков жидкой среды, гравитационного поля, поля центробежных сил, ультразвукового поля, механических вибраций, броуновского движения. В частности, было обнаружено влияние электрического поля, возникающего при оседании мелких частнц, на скорость седиментации. В. Г. Левнчем и А Н. Фрумкиным было указано, что вблизи поверхности капли, движущейся в жидкой среде, может возникать электрическое поле диффузионного происхождения. Поляризация ионных слоев, наступающая вследствие деформации двойного электрического слоя, обусловливает проявление дальнодействующих снл притяжения между индуцированными диполями. Наконец, Штауф наблюдал • образование периодических структур из непроводящих коллоидных частиц, находящихся в переменном электрическом поле. Некоторые из этнх эффектов более подробно рассмотрены в гл. IX.
 1 ноября, 2012
1 ноября, 2012  admin
admin 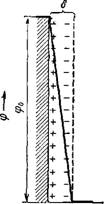
 Опубликовано в рубрике
Опубликовано в рубрике 