Согласно молекулярно-кинетическои теории газ представляет собою совокупность молекул или атомов, находящихся в хаотическом движении Средние расстояния между молекулами в газах значительно превосходят линейные размеры молекул, а суммарный объем, занимаемый собственно молекулами, ничтожен по сраинеиию с объемом газа Соударяясь друг с другом, молекулы газа изменяют скорость и направление своего движения, однако их средняя кинетическая энергия, зависящая только от температуры, остается всегда неизменной и равной *kkT (где k — постоянная Больцмана, Т—абсолютная температура).
В твердых кристаллических телах молекулы, атомы или ионы расположены в определенном порядке, отвечающем наименьшему значению свободной энергии, и колеблются около положений равновесия — узлов кристаллической решетки
Жидкости по своим свойствам занимают промежуточное положение между газами и твердыми телами По плотности они близки к твердым телам — расстояния между молекулами в жидкости почти так же малы, как в кристаллах, и близки к размерам самих молекул Однако молекулы жидкости, как и молекулы газа, способны менять свои места, правда, не выходя из сферы влияния молекулярных сил соседних молекул
Ранее считалось, что молекулы в жидкости расположены беспорядочно по отношению друг к другу Однако рентгенографические исследования показали, что в весьма малых областях жидкости имеется определенный порядок расположения молекул Принято считать, что структура жидкости характеризуется ближним порядком в отличие от кристаллов, которым свойственен дальний порядок При этом следует учитывать, что области с квазикристаллическим порядком в жидкости во времени не постоянны, — возникнув в одном месте и просуществовав очень недолго, они распадаются и образуются в другом месте.
Согласно современной теории жидкостей, предложенной Я И Френкелем н независимо от него Эйрингом, передвижение молекул в жидкости совершается таким образом, что когда какая-нибудь молекула меняет свое место, происходит перегруппировка соседних молекул и эта перегруппировка продолжается до тех пор, пока каждая молекула снова не займет положение, наиболее выгодное в энергетическом отношении Рассмотрим представления Я И Фредкеля несколько подробнее
Наличие ближнего и отсутствие дальнего порядка в жидкости указывает на то, что в ее молекулярной упаковке имеются пустоты, нли дырки Повышение температуры способствует увеличению числа дырок и уменьшению ква- знкристаллической упорядоченности Наличие дырок и обусловливает способность жидкости к течению и увеличению объема при плавлении
Многие молекулы жидкости могут оказаться расположенными по соседству с дырками, как изображено на рис 111, 1 В энергетическом отношении такнё молекулы находятся в потенциальной яме и отделены от других возможных равновесных положений энергетическим барьером Однако каждая из этих молекул, если она обладает достаточной энергией, может совершить скачок и занять находящуюся рядом дырку, перейдя в новое положение равновесия Естественно, что в результате такого скачка молекула оставит после себя дырку.
В которую в свою очередь может перескочить другая молекула. Число возможных скачков будет тем больше, чем больше число дырок н чем меньше высота энергетического барьера, который должна преодолеть молекула прн переходе нз одного положения равновесия в другое.
Такое перескакивание молекул, очевидно, определяет возможность нх теплового перемещения в жидкости, нлн самоднффузнн. Прн увелнчеинн температуры скорость самоднффузнн возрастает, так как прн этом молекула, расположенная рядом с дыркой, имеет большую вероятность приобрести энергию, необходимую для преодоления энергетического барьера Помимо этого скорость диффузии растет с температурой нз-за увеличения числа дырок в результате термического расширения жидкости Мнинмальиая энергия, необходимая для того, чтобы молекула жидкости могла переместиться нз одного временного положения равновесия в другое, называется анергией активации диффузии. Эта величина зависит от компактности упаковки молекул, нх размера н от межмолекуляриых снл.
В рассмотреинном выше случае самоднффузнн прн отсутствии виешиого силового поля скачкн молекул одинаково часты во всех направленнях, н поэтому подобный процесс не приводит к переносу вещества в каком-инбудь преимущественно одном направлении. Прн иалнчнн внешнего силового поля, например напряжения сдвига, более вероятен скачок в направлении действия поля, так как не- иеобходимая для этого энергия активации будет меньше, чем для скачка в противоположном направлении. В результате произойдет вынужденная днффузня, обусловливающая вязкое течение жидкости (последнее рассмотрено в гл. X).
Аналогично объясняется а днффузня молекул вещества, растворенного в жидкости. Молекулы вещества в растворе, совершая скачкн примерно таким же образом, как н молекулы растворителя, в силу беспорядочности движения не могут оставаться в каком-либо определенном месте, а распределяются в среднем равномерно по всему объему жидкости. Согласно термодинамике это соответствует увеличению эитропнн системы.
Можно сказать, что тепловое движение каждой молекулы жидкости состоит частично нз колебательных движений около положення равновесия н частично нз небольших поступательных движений, когда под влиянием особо сильного удара соседней молекулы нлн нескольких случайных ударов в близких друг другу направленнях молекула настолько далеко удаляется от равновесного положення, что оказывается ближе к некоторому новому положению равновесия. Таким образом, все молекулы жидкости как бы ведут кочевую жнзиь, причем кратковременные «переезды» (скачкн нз одного положення равновесия в другое) сменяются относительно продолжительными периодами «оседлой жнзин» (колебание вокруг положення равновесия). Именно сравнительно длительными периодами «оседлого» существования молекул в жидкостях объясняется, что днффузня в жидкостях происходит гораздо медленнее, чем в газах.
Важно отметить, что при высоких температурах жидкости по свонм свойствам приближаются к газам В критическом состоянии различие между жидкостью и газом исчезает, а прн температурах выше критической жидкость превращается в газ. Наоборот, при низких температурах, близких к температурам кристаллизации, жидкости по свонм свойствам приближаются к кристалла^. Однако переход жидкости в кристаллическое состояние всегда происходит скачкообразно Когда жидкости по тем или ниым причинам ие могут перейти в кристаллическое состояние, оин с понижением температуры переходят в стеклообразное (аморфное) состояние
|
|
|
Рис. Ш, 1. Схема расположения молекул вблизи дырки. |
Тепловое движение частиц в коллоидных и микрогетерогенных •системах получило название броуновского движения в честь анг — лТгйсКого ботаника Р. Броуна, обнаружившего его в 1827 г. при
наблюдении под микроскопом водной суспензии цветочной пыльцы. Броун не смог объяснить природу этого явления, но установил, что движение частиц пыльцы не ослабевает со временем, не зависит от внешних источников энергии (света, сотрясений) и тем интенсивнее, чем выше температура. Позднее разные исследователи пытались объяснить броуновское движение жизнедеятельностью пыльцы, наличием конвекционных токов в системе, электрическими явлениями, неравномерным смачиванием частиц средой. Однако первое предположение пришлось отбросить, так как броуновское движение оказалось свойственным не только суспензии пыльцы, но и вообще всем суспензиям, в том числе и суспензиям неорганических веществ. Объяснение броуновского движения существованием в жидкости микроскопических конвекционных токов оказалось несостоятельным, так как при этом соседние частицы должны были бы передвигаться с одинаковой скоростью и параллельно друг другу. На самом же деле микроскопическое наблюдение показывает, что соседние частицы движутся с различными скоростями по траекториям, пересекающимся под разными углами. Несостоятельными оказались и объяснения броуновского движения с помощью электрических сил и неодинакового смачивания поверхности частиц дисперсионной средой.
Гуи (1888 г.) и Экснер (1900 г.) предположили, что броуновское движение имеет молекулярно-кинетическую природу, т. е. является следствием теплового движения. Правильность этой точки зрения была подтверждена теоретическими расчетами Эйнштейна и Смолуховского и экспериментальными работами Перрена, Свед — берга и ряда других исследователей. Теперь точно установлено, что движение коллоидных частиц является следствием беспорядочных ударов, наносимых им молекулами среды, находящимися в тепловом движении. Если частица достаточно мала, то число ударов на нее приходящихся с разных сторон обычно неодинаково и частица получает периодические импульсы, заставляющие ее двигаться в разных направлениях по очень сложной траектории. С увеличением размера и массы частицы вероятность компенсации ударов возрастает, а инерция частицы становится больше. Это приводит к тому, что большие частицы, порядка 5 мкм, совершают движения, воспринимаемые нами как колебания около некоторого центра. При диаметре частицы больше 5 мкм броуновское движение практически прекращается.
Следует указать, что кроме поступательного движения малые частицы вследствие ударов молекул претерпевают и вращательное броуновское движение.
В результате огромного числа ударов, которые наносят молекулы среды коллоидной частице, последняя меняет свое направление и скорость весьма часто. За одну секунду коллоиДная частица может изменить свое направление свыше 1020 раз. В таких условиях определить истинный путь коллоидной частицы невозможно, но легко определить среднее расстояние, на которое она
Смещается в единицу времени. На рис. 111,2 схематически пред — ‘ ставлена проекция движения частицы на плоскость. Эту проекцию можно найти, наблюдая броуновское движение одной частицы в микроскопе и регистрируя ее положение в поле зрения через равные промежутки времени. При этом движение частицы от одного зарегистрированного положения до другого только условно изображено прямой линией. На самом деле оно также имеет ‘ весьма сложную зигзагообразную траекторию в пространстве. Поскольку обычно интересуются передвижением частицы в каком-нибудь определенном направлении (например, в направлении, в котором идет диффузия), то для количественных расчетов, о которых речь будет идти ниже, берут не само_смещение, или сдвиг, а величину А, представляющую среднее квадратичное значение проекции смещения частицы на ось х, параллельную выбранному направлению. Среднеарифметическим значением проекции смещения пользоваться нельзя, так как вследствие равной вероятности всех направлений движения частицы оно равно нулю. Среднее квадратичное значение проекции смещения находится из уравнения: ________________
_ ^ /д| + д1 + д1+ … л = Д/ —— (ПІ, 1)
Где Ді, Дг, Аз… — отдельные проекцнн смещения частицы на ось х; п — число таких проекиий, взятых для расчета
 1 ноября, 2012
1 ноября, 2012  admin
admin 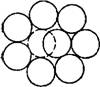
 Опубликовано в рубрике
Опубликовано в рубрике 