^-Структуры. В работе [386] рассматривается вопрос о том, отражают ли мгновенные структуры, получаемые в процессе численного моделирования, наиболее фундаментальные особенности структуры исследуемых систем — кристаллических, жидких, аморфных и т: д. Так, мгновенные /-структуры (по терминологии Дж. Эйзенберга и В. Кауцмана [387]) кристаллов не обладают, строго говоря, ни симметрией, — ни периодичностью. Для того чтобы выявить эти присущие кристаллическому состоянию особенности, необходимо рассматривать идеализированные, например усредненные по колебаниям атомов, структуры (У-струк — туры по [387]). Ю. И. Наберухин и соавт. [388] предлагают обобщить понятие V-структур на случай систем со сложным механизмом подвижности молекул, не позволяющим получить простым усреднением координат физически оправданные структуры. Одним из алгоритмов получения таких идеализированных структур, которые авторы работы [388] предлагают называть собственными, является поиск ближайшего к данной мгновенной структуре минимума потенциальной энергии. В рамках численного эксперимента такой поиск может заключаться в резком понижении температуры моделируемой системы. Полученные таким образом структуры предлагается называть /7-структура — ми [386, 388]. /"-Структуры являются одной из разновидностей собственных структур. Аналогичный подход развивается в работах Ф. Стиллинджера и Т. Вебера [389—391]. Эти авторы предпочитают использовать термины «существенные» или «скрытые» структуры. Подчеркивая роль этих исследований в разработке концепции собственных структур, автор предлагает называть областями Стиллинджера — Вебера области в конфигурационном пространстве, соответствующие данной собственной структуре (например, /"-структуре) [386].
Таким образом, в исследовании структуры любой конденсированной фазы можно выделить два уровня: 1) изучение собственных структур и 2) изучение их термических возбуждений или флуктуаций (мгновенных структур). В случае структур кристаллических объектов эти уровни описания называют иногда статическими (1) и динамическими (2) структурами (см. например, работу [392]). Ниже мы проиллюстрируем эффективность такого подхода к структурам некристаллических объектов — кластеров, содержащих молекулы воды.
Нами было предпринято моделирование кластеров (Н20)п (п = 2-^20) с помощью одного из наиболее распространенных методов численного эксперимента — метода Монте-Карло. При этом использовалась стандартная процедура Метрополиса и др. [393]. Конкретный вариант этой процедуры описан в других наших публикациях [386, 394—396]. Расчеты проводили с помощью потенциалов, характеризующих взаимодействие между молекулами воды: потенциалов (1), ([394], см. также [386]) и потенциалов (2), описанных в работе [397]. В первом случае молекулы воды представлены системой четырех точечных зарядов ±0,195 е (е — заряд электрона), расположенных в верши-
Таблица 8.4. Некоторые характеристики
|
Число водородных связей ЛНВ |
|
Тип конфигурации |
|
(2) |
Потенциальная энергия —U, кДж/моль
(1)
|
6 7 9[2] 8 |
|
179,6 177.5 174.6 168.7 |
|
179,6 183,4 187,6 184,2 |
Гексагональное кольцо Два квадрата с общим рядом Тригональная призма Октаэдр
|
F-структур кластеров (Н20)6
|
|
Имеет расстояние /?00=335 пм, так что может считаться разорванной. |
Нескольких, близких по энергиям, конфигураций кластера (Н20)л проиллюстрируем на примере п=6. Характеристики некоторых ^-структур гексамеров из молекул воды приведены в табл. 8.4. При расчетах с потенциалами (1) наиболее выгодным оказывается почти плоское шестичленное кольцо, а при использовании потенциалов (2) преимущественно устойчивы структуры с максимально большим числом водородных связей, хотя и искаженных, углы между которыми сильно отличаются от тет — раэдрических.
Среди кластеров (Н20)в наиболее устойчивы такие, в которых молекулы расположены по углам лишь незначительно искаженного куба. В этих кластерах каждая молекула участвует в образовании трех водородных связей. В табл. 8.5 приводятся данные для кубического кластера, содержащего 12 водородных связей, и для октамера Стиллинджера — Дэвиса с девятью водородными связями.
Таким образом, потенциал MCY, широко используемый для моделирования водных систем [379], дает для кубического кластера результаты, близкие к полученным с нашими экспериментальными потенциалами (1) и (2). Что касается поляризацион-
|
Таблица 8.5. Некоторые F-структуры кластеров (Н20)ь
|
Ной модели, то она не была использована для расчета кубического кластера.
Итак, на поставленный выше вопрос, что лучше: больше «плохих» водородных связей или меньше «хороших», окончательного ответа дать нельзя. По-видимому, циклические триме — ры в действительности не являются столь стабильными, как это следует из расчетов с потенциалами (2) (см. табл. 8.3), а, следовательно, и кластеры, содержащие такие тримеры (см. две последние строки в табл. 8.4).
/-Структуры. Результатом численного эксперимента является набор конфигураций моделируемой системы, т. е. набор /-структур. Чтобы этот набор был представительным, необходимо, чтобы он содержал достаточно большое количество /-структур (по крайней мере, несколько сот тысяч), относящихся ко многим различным областям Стиллинджера — Вебера. Закономерности структуры ансамблей /-структур носят статистический характер и описываются различными функциями распределения.
Моделирование кластеров из молекул воды выполняли многие авторы, начиная с 1974 г. Они использовали различные потенциальные функции и конкретные алгоритмы моделирования [398—405]. В работах [398, 400] применялись методы Монте — Карло, а в работах [399, 401—405] проводили молекулярно-ди- намическое моделирование.
Для интерпретации структурных результатов численных экспериментов очень важен вопрос формального определения водородной связи между молекулами воды. При анализе/-структур водородная связь вообще не может быть определена однозначным образом [386, 405, 406]. Это заключение согласуется с выводом Ю. И. Наберухина о том, что водородная связь может быть строго определена только для собственных структур, в частности, для /"-структур [383]. Тем не менее вопрос о водородных связях в ансамбле /-структур столь важен, что, начиная уже с первых работ по моделированию водных систем, предлагались различные подходы к их поиску. При этом наметились две группы критериев водородных связей: энергетические и геометрические. Согласно геометрическим критериям, любая пара молекул считается соединенной водородной связью, если расстояние между атомами кислорода, угол О—Н… О и (или) расстояние между атомом водорода и атомом кислорода не выходят за пределы некоторых значений, установленных на основании анализа данных о структурах кристаллов. Поскольку структуры кристаллов — это собственные (V) структуры, то прямое перенесение полученных для них зависимостей на мгновенные (/) структуры, собственно говоря, не правомерно. Согласно энергетическим критериям, любая пара молекул, энергия взаимодействия которой ПО модулю больше некоторой величины t»HB, считается соединенной водородной связью. Энергетический крите-
|
Таблица 8.6. Средние числа водородных связей пнв, в которых участвует молекула воды в кластерах (Н20)п, полученные с использованием парных энергетических критериев
|
|
* В оригинальной работе [399] величины энергетического критерия кнв приведены в ккал/моль. |
Рий еще более условен, чем геометрический. Для примера приведем таблицу 8.6, заимствованную из работы [399].
Авторы работы [399] попытались использовать также независимый от критериев способ определения числа водородных связей, основанный на вычислении площади под первым максимумом пика функции распределения расстояния /?он(£он). На условность и неоднозначность методов подобного рода для анализа структурных особенностей ансамблей /-структур уже указывалось ранее [386]. Обратим внимание, что применение «критерия £он» приводит к числу водородных связей, равному или даже большему, чем полученное с энергетическим критерием VHB= = 8,37 кДж/моль (2 ккал/моль). Как показывает опыт численного моделирования, среди пар молекул, энергия взаимодействия которых близка к этому значению, встречаются такие, кон-
ОС
|
Рис. 8.1. Двумерное распределение характеристик, определяющих взаимное Расположение молекул во всех парах молекул кластера (Н20)і3. Показана часть распределения для молекул, расстояние между которыми не превышает 450 пм. Температура моделирования 300 К, потенциалы (1). Средняя потенциальная энергия кластера 308,2 кДж/моль, среднее число водородных связей в кластере (геометрический критерий) 14,2. По оси абсцисс — расстояния О… О в пм, по оси ординат — углы О—Н… О в градусах. Вероятности соответствующих конфигураций показаны отдельно |
Фигурация которых явно не отвечает возможности образования водородной связи.
Условность геометрических критериев наглядно иллюстрирует рис. 8.1, на котором показано двумерное распределение расстояний Roo и углов О—Н… О, полученное нами при моделировании кластера (Н20)і3. Пик этого распределения, отвечающий образованию водородных связей, не имеет четких границ.
Автором и сотр. [405] предложен динамический критерий водородной связи, основанный на анализе не только данной конфигурации, полученной в ходе молекулярно-динамического моделирования, но и ее предыстории и ее дальнейшей «судьбы». Построение временных зависимостей энергий взаимодействия двух молекул в большинстве случаев позволяет судить о том, существует ли прн данной конфигурации водородная связь, в какие моменты времени она возникла и когда была разорвана (рис. 8.2). Как и всегда при рассмотрении ансамбля /-структур, при использовании этого подхода могут возникать сомнительные случаи. Однако такие случаи редки и по степени определенности поиска водородных связей «динамический» критерий приближается к анализу F-структур.
Что касается распределений геометрических характеристик водородных связей в малых кластерах из молекулы воды, то они, при использовании одной и той же модели взаимодействия, мало зависят от числа молекул в кластере и почти не отличаются от полученных при моделировании объемной воды. Так, двумерное распределение, показанное на рис. 8.1, характеризует и кластеры с иным числом молекул воды и объемную воду (моделируемую в численном эксперименте как система с периодическими граничными условиями).
Г, В
О
|
|
|
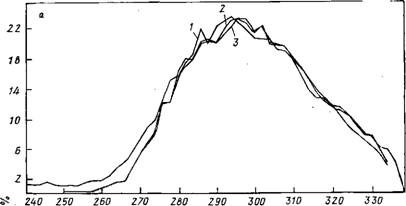
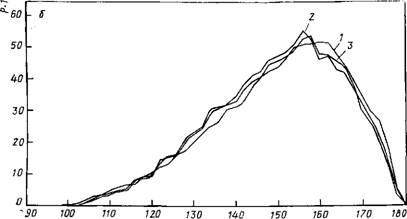
Рис. 8.3. Распределение геометрических характеристик в кластерах: с —расстояний R00 Б — углы О—Н…О. / — кластер (Н20)ю; 2 — Na(H20)i5; 3 — K(HsO)u. Метод Монте-Карло, Г=300 К; / — усреднение по 105 конфигурациям; 2 и 3 — По 1,5- 10s конфигурациям |
|
А, г(лд |
|
На рис. 8.3 показаны одномерные распределения величин Roo И углов О—Н…О, полученные для температуры 300 К. Форма этих распределений, естественно, зависит от температуры [395]. Ее понижение приводит к изменению соответствующих пиков. При температурах ниже 100 К максимум двумерного распределения, отвечающий водородным связям, выявляется четко и оказывается окруженным зоной с почти нулевой вероятностью встречаемости соответствующих конфигураций. Этот результат обосновывает правомерность утверждения, что при рассмотрении |
F-структур (получаемых охлаждением моделируемой системы) выявление водородных связей производится почти однозначно.
Сходство распределений геометрических параметров водородных связей в малых кластерах и в объемной воде приводит к тому, что характер окружения молекул в центральных областях кластера и в объемной воде практически одинаков. Об этом свидетельствует и сходство функций распределения расстояний Roo(Goo), Янн(ённ) И /?он(£он). Разумеется, ограниченный размер кластеров и малое число молекул воды в них сказывается на высоте пиков, отвечающих дальным корреляциям. Так, согласно [399], второй пик на функции Goo вообще не виден для кластеров (H20)g и в меньших, но для кластеров (H20)is он выражен уже достаточно точно.
|
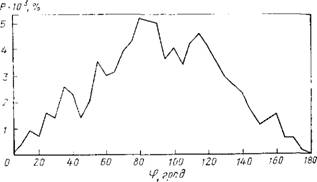
Рис. 8.4. Распределение углов, образуемых дипольным моментом молекулы воды с радиусом-вектором, соединяющим центр системы с атомом кислорода. |
|
Кластер (НгО)ю, Г=300 К, потенциалы (1). Распределение построено для молекул, находящихся в сферическом слое между сферами радиусами 350 и 400 пм. Усреднение по 10s конфигураций |
Но, разумеется, наличие границы сказывается на структуре кластеров. В объемной воде ориентация молекул воды, естественно, хаотична. В кластерах наблюдается преимущественная ориентация диполей молекул параллельно границе кластера [401, 402, 404]. При этом обнаруживается стремление атомов водорода молекул воды находиться на периферии кластера [400, 402, 404]. В проведенных нами численных экспериментах с использованием других потенциальных функций — потенциалов (1) [393] — эти выводы были подтверждены (рис. 8.4); это свидетельствует о том, что количественные результаты численного эксперимента справедливы для широкого класса потенциальных функций. Границы кластеров выражены достаточно четко, о чем свидетельствует резкое спадание их средней плотности на некотором расстоянии от центра масса [402, 404].
 24 октября, 2012
24 октября, 2012  admin
admin 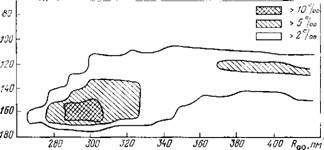
 Опубликовано в рубрике
Опубликовано в рубрике 