Развитые представления об особой структуре граничных слоев и расклинивающем давлении составляют теоретическую основу не только равновесия, но и кинетики тонких водных прослоек и смачивающих пленок.
Начнем рассмотрение процессов массопереноса с простейшего случая однокомпонентной жидкости в тонкой прослойке между незаряженными твердыми поверхностями. Здесь следует учитывать только один эффект, а именно — изменение структуры граничных слоев воды. При течении под действием градиента давления это приводит к необходимости учета послойного распределения вязкости по толщине прослойки Г(х). Если вид этой функции известен, то, решая уравнения Навье — Стокса, легко получить соответствующие выражения для скорости течения и потока в плоской щели или капилляре. В случае гидрофильных пористых тел это приводит к снижению коэффициентов фильтрации, а в случае гидрофобных — к их увеличению.
Термоосмос. Более сложной оказывается ситуация, когда кроме перепада давления АР в прослойке действует также и продольный перепад температуры AT. При небольших отклонениях от состояния равновесия возникающие эффекты удобно рассматривать на основании термодинамики необратимых процессов. Соответствующая система уравнений, где Q и W — удельные потоки массы и энергии, имеет следующий вид:
<7=<хіІАР+Аіг(АТ/Т); (1.4)
Ш=а2ІАР+а22(А7’/Г). (1.5)
Здесь ац — коэффициент изотермической фильтрации; а-ш — коэффициент температуропроводности; <Хі2=<Х2і — перекрестные коэффициенты, равные друг другу, по Онзагеру. Первый из них характеризует термоосмотическое течение в прослойке 9г (при ДР=0), второй — так называемое тепло пере — лоса w0 (при ДГ=0).
Причиной, порождающей термоосмос, является изменение удельной энтальпии АН(х) воды в структурно-измененной тонкой прослойке по сравнению с объемной водой [52]. Изотермическое течение воды в прослойке под действием АР сопровождается поэтому выделением (или поглощением, в зависимости от знака АН) тепла на входе в прослойку и обратным тепловым эффектом на выходе из нее. Количество выделяемого в единицу времени тепла пропорционально скорости течения. Для плоской щели толщиной H тепло переноса (на единицу ширины щели) составит:
1 H. ■
W0=^ AH(x)v(x)dx = anAP, (1.6)
О
Где и (х) — локальная скорость течения.
Уравнение (1.6) позволяет найти коэффициент аіг, характеризующий скорость термоосмоса:
‘ H
«із = = [AH(x)v(x)dx /АР/1. (1.7)
AH(x)v(x)dx
Точные количественные расчеты по этому уравнению требуют установления аналитического вида функций АН(х) и V(X). Надежды на их получение связаны с дальнейшим развитием машинных методов расчета микроструктуры воды в тонких прослойках. В настоящее время используются асимптотические решения, полученные для двух случаев: 1)при h^hs и 2) при H^Hs, где Hs — толщина граничного слоя с измененными свойствами. В первом случае можно считать всю прослойку однородной и положить АН(х) =AHS = const, Ti(A🙂 = TiS=const. Принимая затем распределение скоростей в плоской прослойке пуазейле — вым, получим:
H?AHs h? AHs vr
Где I — протяженность прослойки в направлении течения;V Т — градиент температуры; х —так называемый коэффициент термоосмоса.
Во втором случае можно считать, что значения АН=АН, Постоянны в пределах тонкого граничного слоя Hs и Д#=0 за его пределами, т. е. при x^hs и л:< (/г—hb). Тогда вклад в значения интеграла [уравнение (1.7)] дадут только пристенные; слои, для которых в силу h^hs можно принять линейное распределение скоростей течения. В этом приближении, считая г) = const, получим:
H2sMis hAHs х/Т
————————- ; ЧТ*=- Ц$Т V7-=.x—JT-. (1.9>
Как видно из выражений (1.8) и (1.9), эффект термоосмоса исчезает при АН=0 или при Hs = 0. Направление термоосмоса зависит от знака АН. При АН<0 (т. е. при условии, что межмолекулярная водородная связь в прослойке в среднем прочнее, чем в объемной воде) поток <7г>0 направлен в горячую сторону. Ослабление Н-связей в водной прослойке должно вызывать термоосмотическое течение, направленное в холодную сторону. Таким образом, наблюдения термоосмоса служат прямым источником информации о характере структурных изменений воды в тонких прослойках и порах.
Измерения термоосмоса в пористых стеклах показали [23], что в широких порах (г>50 нм), где граничные слои еще не перекрыты, ДЖО. Это значит, что структура воды в одиночных граничных слоях укреплена по сравнению с объемной. Напротив, в тонких порах (г<10 нм) рассчитанные по уравнению (1.8) средние значения АН были положительными. Это говорит о преобладающем влиянии эффекта ослабления межмолекулярных связей при перекрытии граничных слоев.
Повышение температуры приводит к постепенному снижению скорости термоосмоса. При температуре выше 60 °С термоосмотическое течение практически прекращается, что свидетельствует об уменьшении различий в структуре воды граничных слоев и объемной воды.
Полученные для пористых стекол значения коэффициентов термоосмоса при комнатной температуре составляют % = —10~6-=- — г — Ю-7 см2/с. Они близки к значениям %, полученным для мембран и глин. Хотя всем этим пористым телам в контакте с водой присущ поверхностный заряд, его влияние не проявляется заметным образом в силу того, что для воды в тонких порах (г<10 нм) xr<c 1. Как известно, в этом случае электрокинетические эффекты заметно не проявляются.
В более широкопористых телах, при хг~1, следует дополнительно учитывать термопотоки, связанные с термодиффузией: ионов и поляризацией воды в поле ДЭС [53].
Электроосмос. При рассмотрении электрокинетических явлений в гидрофильных и гидрофобных капиллярах и порах возникает необходимость учета структурных изменений граничных слоев воды и, прежде всего, изменений вязкости, влияющих на конвективный перенос ионов в ДЭС [54]. При расчете соот
ветствующих поправок было принято, что вязкость экспоненциально изменяется При Приближении К поверхности (г)о — вязкость объемной воды):
П(д:)=тіо/[1 — аехр (-Ьх) (1.10)
Параметры этого распределения были определены на основании приведенной на рис. 1.1 зависимости средней вязкости воды от радиуса капилляров: а = 0,465 и Ь = 6,25-105 см-1. Учет повышенной вязкости граничных слоев воды приводит к модифицированному уравнению Гельмгольца — Смолуховского для потенциала течения ДЕ:
1- И І, (і-")
Где г|), — потенциал поверхности; АР — перепад давления; К. — удельная электропроводность раствора в порах; Ul’=eztyllkT — безразмерный потенциал.
Значения G зависят от соотношения толщины слоев — граничного (1/6) и ДЭС (1/х):
~ [Th(^/4)]»"
І+2п+(Ь/к) • (
Введение поправки на повышенную вязкость граничного слоя воды приводит к повышению действительных значений •фі по сравнению с значениями г|)*, которые определены без учета этой поправки. На рис. 1.8 (кривые 1 и 2) приведены графики, позволяющие определить действительные значения потенциала поверхности г|)і по найденным обычным методом значениям г|)* из уравнения
Д£/ДР=е0ф* /4яг|о/С*.
Чем выше значения фь тем больше относительная величина поправки. С понижением концентрации электролита поправка уменьшается в связи с выходом части диффузного слоя про — тивоионов за пределы граничного слоя.
Кривыми 3 и 4 на рис. 1.8 показаны зависимости і|>і(г|>*), учитывающие эффект скольжения — понижения вязкости воды вблизи гидрофобных поверхностей. В этом случае поправка особенно велика, так как резко повышается скорость конвективного переноса ионов в ближайших к поверхности слоях, где плотность объемного заряда наибольшая.
Введение этих поправок при электрокинетических измерениях в отдельных гидрофильных и гидрофобизованных кварцевых капиллярах привело к результатам, лучше согласующимся с представлениями о формировании поверхностного заряда [54].
Рис. 1.8. Пересчет измеренных значений потенциала поверхности (ф,) в действительные (фі) с учетом измененной вязкости граничных слоев водных растворов-
1-1-электролита: С0= 10—4 моль/л (кривые 1 и 3); С о= =2-Ю-5 (кривые 2 и 4)
Последовательный учет структурных изменений граничных слоев потребует введения в теорию ДЭС (и тем самым в теорию электрокинетических эффектов) представлений об измененной диэлектрической проницаемости воды. Этот новый подход развивается в работах [55, 56].
Капиллярный осмос. Явление капиллярного осмоса, открытое Б. В. Дерягиным [57], состоит в том, что жидкость в капиллярах и порах способна перемещаться под действием градиента концентрации раствора. Причиной капиллярного осмоса является диффузность адсорбционных слоев растворенного компонента. Увлечение потоком жидкости подвижной части диффузных слоев с повышенной (или пониженной) концентрацией С(х) растворенного вещества приводит к возникновению градиента концентрации. В соответствии с уравнениями термодинамики необратимых процессов это обусловливает возможность перекрестного эффекта, а именно — течения жидкости под действием перепада концентраций. В связи с тем что граничные слои воды вблизи гидрофильных поверхностей обладают пониженной растворяющей способностью, толщина диффузных слоев того же порядка, что и толщина граничных слоев. В соответствии с теорией [57], это может заметно увеличивать скорость капиллярно-осмотического скольжения, равную
Оо
RT Г Г С(х) "1 ,
Vt= gradC И—1 Xdx, (1.13)
*о
Где Со (моль/см3) — концентрация объемного раствора за пределами диффузного слоя; х0 — координата плоскости скольжения (начало подвижной части диффузного слоя).
В общем случае здесь следовало бы учесть повышенную ВЯЗКОСТЬ граничного СЛОЯ Л^ЛО, ЧТО приведет к уменьшению значений V.
|
|
В дальнейшем была развита теория капиллярного осмоса растворов электролитов, что позволило разделить эффекты, связанные с ионными и молекулярными диффузными слоями
[58, 59], которые, как правило, одновременно возникают в гидрофильных пористых телах, заполненных водными растворами.
Тонкие поры, где происходит перекрытие диффузных адсорбционных слоев, требуют особого рассмотрения. В этом случае концентрация раствора С(х) ни в одной части поры не равна концентрации объемного раствора С0. Здесь становится неприменимым представление о течении типа скольжения, которое имеет место в широких порах, где толщина слоя с измененной концентрацией много меньше ширины поры. В тонких (в указанном смысле) порах следует учитывать изменение локальных скоростей течения по всей толщине прослойки. Для неионных растворов в плоском канале решение, полученное на основе уравнений термодинамики необратимых процессов, имеет следующий вид [60]:
H
RT Г /і3 с С(х) І
—B&FfadCL~E— J — сГ<А-*>*Л] (1Л4)
О
(h — ширина плоской поры). При h-+oo уравнение (1.14) переходит в (1.13).
Направление капиллярно-осмотического потока зависит от величины отношения C(X)JCo. При положительной адсорбции, когда С(х)>С0, течение направлено в сторону меньшей концентрации раствора. При отрицательной адсорбции раствор течет в сторону более высокой концентрации. Когда гидрофильные поры очень тонки, они практически не содержат растворенного вещества, как это имеет место, например, в случае высокоселективных обратноосмотических и полупроницаемых мембран. В этом случае С(х)= 0, и уравнение (1.14) переходит просто в уравнение для пуазейлевского потока под действием перепада осмотического давления, равного RTAC:
H? RT
V<= — 12r)o grad С. (1.15)
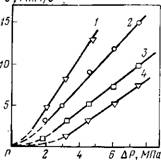
Рис. 1.9 демонстрирует влияние капиллярного осмоса на течение растворов через обратноосмотические мембраны под действием перепада гидростатического давления ДР. В этих опытах совместно проявляются оба эффекта: обратный осмос и капиллярный осмос. Вследствие пониженной (из-за отрицательной адсорбции) концентрации раствора в порах при фильтрации возникает градиент концентрации раствора (обратный осмос): концентрация вытекающего раствора Cf ниже концентрации раствора С0, подаваемого на вход тонкопористой мембраны. Возникающая при этом разность концентраций ДС вызывает капиллярно-осмотическое течение раствора, наклады-
Рис. 1.9. Зависимости скорости фильтрации растворов через тонкопористые обратноос — мотические мембраны (v) от приложенного перепада давления (ДР):
1 — 0,1 М КС1; 2 — 1 М КС1; 3-ІМ ВаС12; 4 — 1 М LaCl3
Вающееся на фильтрационный пуа — зейлевский поток. В случае отрицательной адсорбции, как было показано выше, капиллярно-осмотический поток направлен в сторону более высокой концентрации раствора, т. е. навстречу фильтрационному потоку, вызывая уменьшение скорости течения жидкости.
Как видно из рис. 1.9, капиллярно-осмотическое торможение приводит к тому, что продолжение линейных участков зависимостей V(AP) не проходит через начало координат и отсекает на оси давления отрезок, численно равный так называемому динамическому осмотическому давлению Дя. Для полупроницаемых мембран, когда в порах находится только растворитель (С=0), Дя = Дяо = RTAC. В случае обратноосмотических мембран, в поры которых растворенное вещество проникает (С=^=0), Дя = аДяо. В первом приближении а=<р2<1, где ср = 1— — (Cf/CО) — коэффициент селективности мембраны. Давление Дя является динамическим в том смысле, что оно возникает только при течении раствора. В отсутствие течения разность концентраций снимается диффузией растворенного вещества через поры мембраны.
Для реализации давления Дл скорость течения должна быть достаточно высокой для того, чтобы влияние диффузии было подавлено. Значения внутреннего критерия Пекле должны быть больше 1. При малой скорости течения зависимости и(ДР) становятся нелинейными и приближаются к началу координат так, как это показано штриховыми линиями на рис. 1.9. Для высокоселективных мембран значения а приближаются к 1. Увеличение размеров пор мембраны, приводящее к снижению ее селективности, уменьшает значения а. Так, для мембран из пористого стекла со средним радиусом пор г = = 0,6 нм а = 0,98, а при увеличении г до 1,85 нм значения а снижаются до 0,4.
|
|
Пленочное течение. Особенности кинетических процессов в смачивающих пленках связаны с подвижностью поверхности пленки, граничащей с газовой фазой. Если в тонких порах локально-действующее расклинивающее давление уравновешивается упругими напряжениями в твердой фазе пористого тела, то в смачивающих пленках градиент расклинивающего
давления, не будучи уравновешенным внешним давлением, порождает градиент толщины пленки и ее течение. Разнообразие реализующихся при этом ситуаций определяется видом изотерм расклинивающего давления пленок П(А).
Для многих реальных случаев, которые будут рассмотрены ниже, давление газа над пленкой можно считать постоянным, а влиянием силы тяжести и капиллярного давления можно пренебречь по сравнению с градиентом расклинивающего давления. Это позволяет в уравнения течения смачивающих пленок ввести в качестве градиента гидродинамического давления градиент расклинивающего давления, взятый с обратным знаком, или градиент толщины пленки:
Grad Р=— grad П(/і) =— f(h) grad h, (1.16)
{вид функции F(H)=DU/Dh определяется видом изотермы П(А)]. В области устойчивого состояния пленок (т. е. при DU/Dh<0) течение в пленке направлено от больших ее толщин в сторону меньших. В области неустойчивости происходит переток жидкости в сторону утолщенных участков с тенденцией к прорыву пленки и появлению капель на подложке.
Для смачивающих пленок на плоской подложке применимо уравнение для потока Q на единицу ширины пленки такое же, как и уравнение, описывающее течение через одну из половин плоской прослойки:
Р № pft2 Я=* -%j-grad P^^gradU(h). (1.17)
Это уравнение применимо в отсутствие на поверхности пленка — газ тангенциального напряжения, т. е. при т(А)=0.
Для одномерного потока в пленке с плавно меняющейся кривизной К поверхности жидкость — газ (когда K~D2Hfdx2) Применимо следующее уравнение:
Р/і2 Г dll(h) d*h 1
В случае летучих жидкостей следует учитывать, что градиент толщины и градиент расклинивающего давления в текущей пленке вызовут неравномерное распределение парциального давления пара над ее поверхностью; к течению в жидкой фазе добавится перенос влаги в фазе пара.
При решении задач кинетики для пористых тел, где скорости течения пленок обычно невелики, можно пользоваться условием локального равновесия пленка — пар:
VmTl(h)=— RTn (р/р,), (1.19)
Где vm=l8 см3/моль — объем моля воды.
|
|
|
Q |
|
0 |
Рис. 1.10. Влияние пленочного течения воды на испарение из тонких капилляров
Покажем в качестве примера, как рассчитывается скорость испарения воды из капилляров с учетом диффузии пара и пленочного течения [45]. Будем решать эту задачу в квазистационарном приближении. Пусть мениск находится на расстоянии L от устья капилляра радиуса г полубесконечной длины (рис. 1.10). Рассмотрим испарение в воздух, в котором поддерживается постоянное парциальное давление пара ро = const. В силу условия неразрывности поток массы Q Для каждого сечения капилляра равен сумме потоков в фазе пара Qt, и в пленке Qf.
Q = Qv(x) + Qi(x)
i,RT dx ^ Зг| Где D — коэффициент диффузии пара через воздух; ц — масса моля.
При можно было пренебречь сужением сечения для
Потока пара. В отсутствие пленочного потока (Qf = 0) давление пара линейно спадало бы по длине капилляра в соответствии с уравнением диффузии Фика. Течение в пленке делает распределение р(х)Нелинейным (рис. 1.10). Мгновенную картину распределения давления пара (при данном значении L) можно получить, выразив в (1.20) значение П(х) через р(х) С помощью уравнения (1.19).
|
Nr2D dp 2nrh3(x) dTl |
|
Const, (1.20) |
|
Dx |
Проведя интегрирование уравнения (1.20) в пределах от * = 0 до X = L, получим выражение для скорости испарения при данном значении L:
|
По J /і3(П)Ш, |
|
Q(L) Ряг2 |
|
Р(Ро-Рт) PpRTL |
|
(1.21) |
|
ЗтYL |
Где р — плотность воды; Pm~Ps— давление пара над мениском; П0 и Пт — Расклинивающее давление пленки у устья капилляра и в контакте с мениском.
Значения По И Пщ ОТЛИЧаЮТСЯ ОТ ЗНачеНИИ Пор и Tlmp для плоской пленки на величину капиллярного давления в пленке А/г на цилиндрической поверхности капилляра. При этом П0/» определяется из уравнения (1.19) при р=ро, а Птр = 2А/г.
Скорость испарения при данном L, определяемая уравнением (1.21), выражается через формально взаимно независимые потоки пара Qv и пленочной жидкости Qf. Однако в действительности эти потоки взаимосвязаны: вода испаряется с поверхности пленки внутри капилляра, вследствие чего поддерживается заданное уравнением (1.20) распределение давления пара. Р(х). Распределение потоков в фазе пара QP(x) и в жидкой пленке Qf(X) по длине канала капилляра схематически изображено на рис. 1.10 (внизу). При приближении к устью капилляра растет вклад потока в фазе пара в связи с ростом градиента dp/dx. В связи с тем что при понижении p/ps (и росте П) толщина пленок уменьшается, величина второго члена в уравнении (1.20), характеризующего пленочный ноток, резко снижается. Следует отметить, что жидкость в узких капиллярах практически не испаряется с поверхности мениска. Испарение- происходит с поверхности пленки, отсасывающей жидкость — из-под мениска.
Как видно из уравнения (1.21), влияние пленочного течения тем больше, чем меньше радиус капилляра г и чем меньше разность р0—Рт, определяющая вклад потока пара. Эти выводы теории хорошо подтверждаются экспериментально [45].
Условия течения смачивающих пленок существенно меняются, если к их поверхности, граничащей с газом, приложено» тангенциальное напряжение т. Оно может передаваться пленке, например, под действием обдувающего потока газа или создаваться градиентом поверхностного натяжения пленки T=grada, вызванным температурной или концентрационной зависимостью — А.
Течение смачивающих пленок под действием x=grada(T) носит название термокапиллярного течения [61]. Оно исследовано путем измерения скоростей смещения пузырьков газа в тонких цилиндрических капиллярах под действием постоянного градиента температуры УГ = const. Смещение пузырька; происходит в результате перегонки пара на холодный мениск и термокапиллярного течения пленки, также направленного в холодную сторону, так как (да/дТ)<0. Скорость термокапиллярного течения, пересчитанная на скорость смещения пузырька vT=qT(2nrh/nr2) равна:
H2 f да
^—^(-^Jgrad Т. (1.22),
Для более точного измерения vT небходимо снизить вклад потока пара vv в экспериментально измеряемую скорость смещения пузырька
V—dx/dt = vv + VT.
Это достигается либо понижением средней температуры жидкости, либо повышением давления газа в пузырьке путем запайки частично заполненного жидкостью капилляра в атмосфере азота при давлении до (4—5) • 106 Па.
Экспериментальная проверка уравнения (1.22) проведена для смачивающих а-пленок воды на поверхности кварцевых капилляров на участке между менисками, находящимися при различной температуре [62]. По известным для воды значениям (да/дТ) = —1,6-10-6 Нсм_1-град~’ и известным из опытов г и grad Т можно было определить отношение H2/R. Принимая для тонких пленок т]=1,5т]о, где г)о — вязкость объемной воды, для серии из 16 опытов в капиллярах радиусом от 1 до 10 мкм были получены значения H в интервале от 5 до 10 нм, что близко к эллипсометрическим оценкам толщины а-пленок [45]. Разброс значений толщины (от 5 до 10 нм) связан в данном случае с влиянием гистерезиса краевого угла — неполным смачиванием объемной водой а-пленок. Для объяснения наблюдавшегося разброса достаточно допустить, что наступающий угол 0д составляет 8—10°, а отступающий угол 0R близок к 0°, что согласуется с известными экспериментальными данными.
Теория электроосмоса смачивающих пленок воды была развита применительно к случаю, когда заряд на поверхности пленок, граничащей с газом, отсутствует [45]. Это позволяло использовать известные злектрокинетические решения для плоских щелей с одинаковыми потенциалом и зарядом обеих поверхностей. Электроосмотический поток в пленке получался при этом таким же, как в одной из половин симметричной щели. Возможность такого подхода определялась равенством нулю напряжения сдвига т на поверхности пленки. В действительности же заряд свободной поверхности смачивающих пленок чаще всего отличен от нуля, что связано с адсорбцией ионов или молекул ионогенных ПАВ. При наличии поверхностного заряда пленки Q на ее поверхности возникает тангенциальное напряжение t=QVЈ, где VЈ—градиент электрического поля.
Учет заряда приводит к изменению уравнений для электроосмотического течения пленки, в которые теперь входят значения потенциала и заряда обеих поверхностей пленки [63]. Наличие поверхностного заряда может (в зависимости от его величины и знака) ускорять или тормозить электроосмотическое течение пленок по сравнению со случаем, когда т = 0. Экспериментально электроосмотическое течение пленок изучено еще недостаточно.
Как видно из сделанного обзора, свойства воды и кинетика ее переноса в пористых телах отличаются значительным разнообразием и зависят как от свойств твердых поверхностей, с которыми контактирует вода, так и от состава водного раствора.
Все это открывает широкие возможности управления этими: свойствами в нужном для практики направлении. Изученные^ закономерности течения воды и зависимости ее свойств от различных внешних условий составляют фундаментальную основу для решения различных задач мембранного разделения, флотации, влагообмена в почвах, грунтах и строительных материалах, теории и практики сушки и фильтрации.
 24 октября, 2012
24 октября, 2012  admin
admin 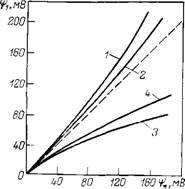

 Опубликовано в рубрике
Опубликовано в рубрике 