Лако-красочные материалы — производство

Для получения полимеров с модифицированными свойствами, сочетающими некоторые свойства различных гомополимеров, используют несколько (обычно два или три) разных мономеров, проводя реакцию их сополимеризации. Изменяя состав сополи­мера, можно влиять на растворимость, температуру размягче­ния, эластичность и на другие свойства. Сополимеры содержат чередующиеся звенья различного состава, и чем значительнее различие в структуре разнородных звеньев, тем сильнее это ска­зывается на свойствах сополимера. Сополимеры в настоящее время находят очень широкое применение в лаках, пластмассах и синтетических каучуках.

Выбирая различные мономеры и способы распределения по­вторяющихся (мономерных) звеньев в структуре макромолекул, можно получить очень широкие возможности синтеза разнооб­разных сополимеров. В простейшем случае, используя всего лишь два мономера Mi и Мг, можно синтезировать сополимеры с существенно различающимися структурами. Макромолекулы сополимеров могут состоять из чередующихся звеньев разных мономеров или из длинных полимерных блоков одного из сомо — номеров.

Чаще всего при обычной радикальной сополимеризацин встречается статистическое распределение звеньев сомономеров: … М1М1М2М|М2М2М1М2М2М2М1М2М1М1М2М1… (1>

Редко образуются сополимеры с регулярным чередованием мономерных звеньев:

… М, Л12М1М2М1М2М1М2М, М2… (II)

Так называемые привитые сополимеры содержат основную полимерную цепь, полученную из одного мономера Мь на кото­рую привиты ковалентно связанные с нею полимерные блоки (ветви) (М2)лг другого мономера:

… М1М1М1М1М1М1М1М1М1М1… (III)

I I I

(Щ)а (ЛШ М2)е

В привитых сополимерах (III) основные цепи могут состоять также из мономера М2, а боковые — из мономера Мь

Блочные сополимеры (блок-сополимеры) характеризуются

Линейным расположением полимерных блоков каждого сомоно — мера (например, М. и М2, М3):

TOC o "1-5" h z (М^о—(М2Ь АВ[2]— блок-сополнмер (IV).

(МО с—(М2)„—(М,)в АВА*— блок-сополимер (V)

(М^п—(Мг)т—(М3), АВС*— блок-сополимер (VI)

При наименовании привитых сополимеров (III) рекомен­дуется применять аббревиатуру слова «привитой», например поли(стирол-яр-бутадиен), а в названиях блок-сополимеров (IV, V, VI)—слово «блок», например поли(стирол-бжж-бута- диен).

В этих названиях первая из обозначенных полимерных по­следовательностей соответствует гомополимеру (или иногда со­полимеру), полученному на первой стадии синтеза. У привитых сополимеров это основная цепь полимера (или сополимера), на которую произведена прививка второго мономера.

Блок- и привитые сополимеры можно получать и методами поликонденсации (полиприсоединения), за счет реакционноспо­собных концевых (нли боковых) функциональных групп поли­мерных цепей.

Разнообразные возможности появляются и при синтезе сме­шанных полимеров типа взаимопроникающих сеток (ВПС), представляющих собой систему из двух (или более) сетчатых полимеров. Входящие в структуры Впс сетчатые гомополи­меры, полученные (чаще всего последовательно) из каждого мономера, связаны между собой не химическими связями, а пу­тем простого механического переплетения сеток. Таким путем

Можно получать смешанные полимеры с разнообразными свой­ствами.

На примере бинарной сополимеризации можно установить зависимость состава исходной смеси мономеров М1 и М2 от мольного содержания их звеньев тх и т2 в сополимерах типа (I) и (II).

В смеси двух мономеров будут протекать четыре различные реакции роста цепи (вместо одной при гомополимеризации). Обозначим растущие радикалы ~М1* и ~М2* (при концевых звеньях соответственно М1 и М2). Каждый радикал может реа­гировать как с мономером Мь так и с мономером М2, причем вероятность этих реакций пропорциональна их константам ско­рости:

Реакции роста цепи Скорости реакций

*1,1

1. ~МГ + М* —М^. ймГМгЦМ!]

*1,2

2. ~МГ +М2 —Л^М*. *1,а[МгНМ*] (1.94)

3. ~М2- +М2 —^ м2м2. Чг[М2-}1М2]

*8,1

4. ~М2- +М, ———- V М2Мг. ft2.1fM2.lfM!]

Мономер М1 участвует в реакциях (1) и (4). Уравнение его расхода может быть выражено следующим образом:

— £г[М1]/с! т=й1,1[М1-] [М,]+Ьл[М*-] [М,]. (1.95)

В реакциях (2) и (3) расходуется мономер М2:

— ^[М2]лгт=£,,2[М,-] [М2]+А2,2[М2-] [М2]. (1.96)

Разделив уравнение (1.95) на (1.96), получим отношение скоростей вступления мономеров в сополимер:

ГЦМ,] | А1,1[М1-][М1] + ^,1[М2-]1М1]

<ЦМ2] Ах,2[М1-][М2] + *22[М2.][М2]

В квазистационарном состоянии концентрации макрорадика­лов Мх* и М2- будут постоянны, поскольку в результате их мно­гократного взаимного превращения установится равновесие.

Следовательно, скорости реакций роста (2) и (4) при равнове­

Сии сравняются в результате их многократного повторения:

*1,2[М,-] [М2]=*2,,[М2.] [М,]. (1.98)

Полученное из уравнения (1.98) значение [Мг*] подставим в уравнение (1.97); числитель и знаменатель правой части пре­образованного уравнения умножим на [М^/й^г. Произведя со­
кращение и приняв, что Гі = кЛІкіЛ и г2 = к2,2/62.ь получим: «ПЛУ [М»](гЕ [МХ] + [М*])

(1.99)

[М2](г2[Л1.]

Отношение б/[М1]/с?[М2] можно заменить на отношение кон­центраций звеньев этих мономеров т1т.1 в образующемся сопо­лимере:

«1 _ +

Тг [М2](г2[М2] + [М1]) • •

Уравнения (1.99) и (1.100) называются уравнениями состава сополимера. Они показывают зависимость состава сополимера (содержание в нем звеньев мономеров т.1 и гп2) от соотношения мономеров в реакционной смеси. Величины п и г2 в этих урав­нениях называются константами относительной активности мо­номеров (константами сополимеризации).

Уравнение (1.100) можно использовать только при низких степенях превращения мономеров в реакционной смеси, т. е. на начальных стадиях сополимеризации (степень завершенности <0,1). Уравнение (1.99) является дифференциальным, поэтому оно пригодно на любой стадии процесса. Точное интегрирование этого уравнения в общем виде невозможно, поэтому, вводя упро­щения, получают его интегральные формы, пригодные для рас­четов.

Характер кривых состава сополимера определяется величина­ми констант сополимеризации (рис. 1.11).

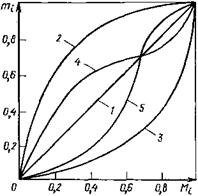При Г1=Г2—1 растущие цепи неизбирательны в реакциях с мономерами М1 и М2, и состав сополимера всегда равен составу исходной реакционной смеси (линия азеотропа 1). Такое соотношение г и г2 является как бы част­ным случаем общей закономерности, при которой г^2—. Последнее равен­ство справедливо при Г1>1 и г2< 1 (сополимер обогащен мономером М1 по всей области составов — кривая 2), или при Г1<1 и г2> 1 (сополимер обо­гащен мономером М2 — кривая 3). Это наблюдается при близкой реакцион­ной способности мономеров по отноше­нию к макрорадикалам обоих типов. Такие системы характеризуются кри­выми 2 и 3, называемыми идеальны­ми (азеотроп не образуется). В том случае, когда г1 и г2 сильно различа­ются по величине (например, п»1, г2<& 1), вначале будет протекать го — мополимернзация одного из мономе-

Рис. 1.11. Зависимость состава сопо­лимера от состава исходной смеси (Ші и М( — мольные доли первого мономера соответственно в сополи­мере и в смеси мономеров):

1 — п=г2=1 (линия азеотропной смеси);

2 — гС> 1, г2< 1; 3 —г,<1. г2> 1; 4 — г,<1. г2< 1; 5 — Гі>1, г2> 1
ров практически до полного его израсходования. В результате может образо­ваться не сополимер, а смесь двух гомополимеров. При способности макрора­дикала к взаимодействию с мономером другого типа соблюдается соотношение ■Г1<1 и гг< 1 (кривая 4). При этом наблюдается тенденция к правильному чередованию мономерных звеньев, причем оно тем регулярнее, чем меньше значения констант сополимеризации. Кривая 4 пересекает линию азеотропной смеси; точка пересечения указывает состав исходной смеси мономеров, отвеча­ющей азеотропной. Для азеотропа характерна идентичность составов исход­ной смеси мономеров и сополимера.

Кривая 5 (г,>1 и г2> 1) характеризует процесс,, когда могут образовать­ся сополимеры, содержащие длинные последовательности из одинаковых звеньев или смесь гомополимеров (Г!»1, г2»1). Это характерно для ионной сополимеризации.