2 января, 2013 
admin Как уже отмечалось выше, к настоящему времени выявлено большое число процессов хемосорбции с переносом части заряда адсорбирующихся частиц на поверхность металла. Термодинамический подход к подобным процессам был намечен еще в [161, где рассматривалась адсорбция атомов водорода на поверхности платины, сопровождающаяся образованием диполей водорода й уменьшением емкости двойного электрического слоя. На основе обобщенного понятия о заряде электрода в последние годы была развита последовательная феноменологическая трактовка переноса заряда при хемосорбции [89—931.
Предположим, что процесс
Ox-f-e^^Red (61)
Протекает через промежуточное адсорбционное состояние А:
Ох + пхе А (62а)
А + п2е Red (626)
Очевидно, пх + щ = 1. Величины % и л2 были названы формальными коэффициентами переноса заряда [92]. При хемосорбции Ox-процесс может остановиться на стадии (62а), а при хемосорбции Red — на стадии (626). Можно показать, что формальные коэффициенты переноса заряда определяются соотношениями
|
(64) |
«1 — — (*270T2)£ = (дТЯей/дТ^)Е (63)
N2 = (dQVdTz)E=idT0jdT2)E
Где rs = Г0х + rRed. Используя уравнение электрокапиллярности обратимого электрода, соотношения (63) и (64) можно преобразовать к виду:
+ F-T-5-! 1 (65)
NA = (агок/дгг)£ = IT IT2*-) + +
^/HRed
Коэффициенты и п% в общем случае отражают не только долю заряда, перешедшего с адсорбированной частицы на электрод (характеризуемую так называемым истинным или микроскопическим коэффициентом переноса заряда к [69]), но и вызванное процессом адсорбции изменение параметров двойного слоя. Именно поэтому /гх и п2 следует называть формальными (термодинамическими) коэффициентами переноса заряда. Соотношения для «х и п2 в случае конкретных редокс-систем приведены в [2, 92].
В работах Феттера и Шульце [94—97] была введена аналогичная щ величина Yit для которой было предложено название «валентность электросорбции». Термин этот менее удачен, чем термин «формальный коэффициент переноса заряда», так как отличные от нуля yt получаются, например, при адсорбции предельных органических соединений на границе ртуть—раствор. Феттер и Шульце нашли величины YL для большого числа адсорбционных процессов. Была сделана попытка на основе модельных соображений выделить из у{ истинный коэффициент переноса заряда к, которая, естественно, выходит за рамки термодинамики [97].
Наиболее ярко на формальный характер пх и п2 и на их отличие от истинных коэффициентов переноса заряда к указывают результаты расчета /ij и п2 для системы Hg, Т1, Т1+, НаО, который был проведен в [74 ] по формулам:
«1 = С5ГТ1 /9Че (6?)
П2 = (дГТ1+/<?Г2)£ (68)
|
Рис. 6. Зависимости пг от потенциала в системе Hg, Т1, Т1+, Н20, рассчитанные различными методами из электрокапиллярных кривых 1-го рода(/, 2) и 2-го рода (/’, 2′, 3′) [74]; |
/ _ [Т1+] = 0,01 М; 2 — [Т1+] = 0,04 М; 1′ — [Tl] = = 0,12% (ат.); 2′ — [Til = 0,68% (ат.); 3′ — [Т1] =4,86% (ат.)
Электрод сравнения тот же, что и для рис. 5.
Приведенные на рис. 6 результаты показывают, что если при положительных потенциалах п2 имеет вполне разумное значение, близкое к 0,75—0,80, то вблизи Е = —0,15 В зависимость П2 от Е терпит разрыв, т. е. п2 ± оо [74].
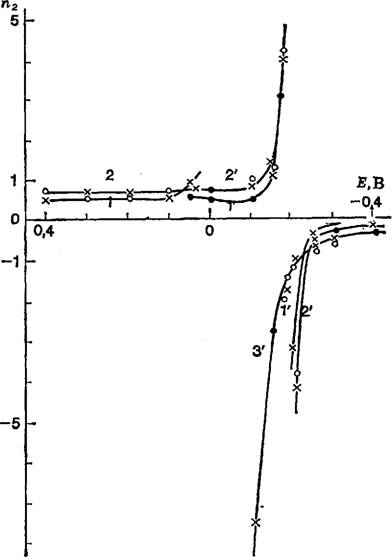
Опубликовано в рубрике 