Рассмотрим теперь вид основного уравнения электрокапиллярности в случае некоторых конкретных обратимых электродов и покажем, каким образом можно экспериментально проверить теорию электрокапиллярности для этих систем.
Наиболее детально к настоящему времени были изучены поверхностные явления на электродах из металлов группы платины [37—55] и на амальгамах таллия [72—75].
На металлах группы платины в некотором интервале потенциалов (так называемая водородная область) могут протекать реакции:
НAd + н20 Н30+ + е (кислые растворы) Wad, + ОН" Н20 —F е (щелочные растворы)
В кислородной области потенциалов на поверхности платиновых металлов происходят процессы:
О Ad + 2Н+ -[- 2е Н20 (кислые растворы) О Ad + Н20 —F 2е 20Н~ (щелочные растворы)
Таким образом, платиновые электроды не являются идеально поляризуемыми, однако в определенном интервале потенциалов их состояние полностью определяется количеством пропущенного через них электричества, что характерно для совершенно поляризуемых электродов [39, 40].
При термодинамическом анализе поверхностных явлений на металлах группы платины в кислых растворах удобно в качестве компонентов при построении поверхностного слоя выбрать атомы водорода Н и молекулы НА, СА и растворителя, т. е.
Незаряженные частицы [41 ] (окончательные результаты от выбора компонентов поверхностного слоя, естестйенно, не зависят). Тогда состояние системы определяется химическими потенциалами атомарного водорода рн, кислоты рНА, соли СА и растворителя. При Г8 = 0 для полного дифференциала обратимой поверхностной работы имеем следующее выражение
Do —ГН DLH — ГНа <*рна — гса <*рса (26)
Где Гн, ГНа» ГСа — гиббсовские адсорбции соответствующих компонентов.
Воспользовавшись условием электронейтральйости
Гна = Гн+; ГСА = Гс+; Гд_ = ГНА+ГСА; Гн+ = ГА_ — Гс+ (27) И соотношением DIH = —DEn Получаем
Do = Гн DEr — Гн+ D^HA — Гс+ DpCA (28)
Где Ег — потенциал, измеренный относительно обратимого водородного электрода в том же растворе.
В случае платиноводородного электрода уравнения (22) и (23) приобретают вид
Q‘ — — Гн = е — Лн (29)
Q" = RH+ = E+Лн+ (30)
И уравнения Липпмана можно записать следующим образом (da/aЈ-WA, »хса = ГН = = — 6 + лн (31)
Дса = = = -8 — Лн+ (32)
Где Е_ — потенциал водородного электрода, измеренный против электрода, обратимого относительно аниона А" в том же растворе.
Уравнение (28) можно переписать в следующем виде
Do = Q’ dEr — Гн+ DiiHA — Гс+ DpCA (33)
И, используя обычные операции над частными производными полного дифференциала, получить ряд термодинамических соотношений, аналогичных (11)—(14):
{W*Ha)B„ ,сд = (дГн+/дЕг)11нАг ^ (34)
{мг/дцHa)Q‘ , ,СА = — (^Гн+/^’),НА, ,СА (35)
На)гн+, иса = — *са (36)
(<?гн+LdEr)Q‘, = (*miHA) гн+. -д (37)
Рассмотрим более подробно уравнение (35). Величина (д-Е/дрнл)*?’, м-са’ вх°Дяш. ая в эт0 уравнение, получила название изоэлектрического сдвига потенциала. Особый интерес представляют следующие частные случаи этого уравнения.
1. v Раствор чистой кислоты (концентрация соли равна нулю: [СА] = 0). При этом, очевидно
(dEr/d^A)Q, = ~2(dTH+/dEr) ± /(dQ’/dEr) (Щ
^НА М- НА
Где р—На — средний химический потенциал ионов кислоты. Для кислоты Н2А
(^R/^IUb* = -3 (dTHiJdEr) ± KdQ‘ldEr) ± (39)
M—HjA/ М-Н2А
Где РН»А — также средний химический потенциал ионов кислоты.
2. Подкисленный раствор нейтральной соли, в котором [СА] > [НА]. В этом случае
ЙцНА = + = DpH+ (40)
„СА = — »cJ(dQ’/dEr)»H+, »CA (41)
Это уравнение справедливо и для раствора соли СЛА, подкисленного НгеА при [СгеА] > [Н„А]. Если относить потенциал электрода к постоянному электроду сравнения, то вместо (41) имеем
UCA = 1 — »СА (42)
А вместо (38)
(дГН+/дЕ) ± / дЕ ^НА
|
^НА |
=1-2 (DQ‘/дЕ) ± (43)
ФЙА ](
В [41, 43] было показано, что область применимости вышеприведенных соотношений может быть распространена на щелочные растворы и на потенциалы, при которых на поверхности электрода адсорбированный водород заменяется адсорбированным кислородом, т. е. на кислородный участок кривой заряжения, если и при адсорбции кислорода систему можно трактовать как обратимую. В [39, 40] были приведены соотношения для электродов, растворяющих водород.
Выведенные термодинамические уравнения позволяют проверить теорию обратимого электрода. Действительно, величины
|
Рис. 1. Сопоставление рассчитанных (сплошные кривые) и опытных (точки) кривых зависимости адсорбции ионов водорода от потенциала платинированного платинового электрода в растворах: 1 — 0,01 н. H2S04; 2 — 0,01 н. НС1; 3— 0,01 н. НВг; 4 — |
(DЈR/Dpha)Q‘ И (дЕг/дцH+)Q‘, ЦСа могут быть найдены методом нзоэлектрических сдвигов потенциала [76]. Величины DQ‘/DEf Можно найти из равновесных кривых заряжения электрода [41 ]. Далее, по соответствующим уравнениям можно рассчитать дТц+1дЕг и, интегрируя (дГН+/д£,.),£г-кривую, найти зависимость АГн+ от Ег. Совпадение рассчитанной АГн+f.^-кривой с полученной на опыте зависимостью Гн+ от Ег укажет на справедливость термодинамической теории и позволит определить интервал потенциалов обратимого поведения системы. Так как константа интегрирования неизвестна, то при сопоставлении расчета и опыта в качестве таковой используют какое — либо одно опытное значение Гн+-
Такая проверка была проведена для многих систем на электродах из платины, палладия, родия, иридия, рутения и сплава платина—рутений (для обзора см. [54, 55]).
Приведенные на рис. 1 примеры, а также результаты проверки теории для других систем показывают, что термодинамическая теория обратимого электрода применима в широком интервале потенциалов, включающем и начальный участок кислородной области. Сильно выраженные явления хемосорбции ионов, при которых процесс образования поверхностного слоя, по-видимому, нельзя рассматривать как полностью обратимый, приводят к сужению области практической применимости теории.
|
(44) |
|
(45) (46) (47) (48) |
|
/лг./лр
|
|
75 |
|
|
|
7 |
|
О |
|
Яг, в |
|
4 |
|
0,01 н. КОН; 5 — 0,01 н. KOH+ 1 н. KC1; 6 —0,01 н. KOH + + 1 н. КВг; 7 — 0,01 н. КОН + 1 н. KI. Кружки — результаты, полученные методом титрования, точки — методом радиоактивных индикаторов [77, 7"8]. ЗиакХ обозначает точки, взятые в качестве константы интегрирования при сопоставлении расчета и опыта. |
|
6 |
Теория была также проверена и для систем, в которых концентрация некоторого иона I, обладающего специфической ад — сор бир у емостью на электроде, была мала по сравнению с концентрацией поверхностно-неактивного электролита, так что химические потенциалы ионов последнего сохранялись практически постоянными при изменении концентрации иона I. В таких условиях
D<7 =- —Q’ DEr — Yi Dpi
Где Г/ — гиббсовская адсорбция поверхностно-активного иона. Из уравнения (44) следует:
(д<2’/дт)Ег= (дТ I/dEr)^ (дЕг! дщ)0. = — №/DQ‘)
(дЕг/дщ)^ =-(DiydQ‘)*R (DTi/DEr)Q, = (DQ‘/Din)Ri Если переписать уравнение (46) в виде
(46а)
То становится ясным, что зависимость адсорбции иона I от потенциала (с точностью до константы интегрирования) можно найти по наклону кривой заряжения и сдвигу потенциала электрода (дЕг! дPJ)Q‘ при изменении концентрации специфически адсорбирующегося иона. Этот сдвиг получил название адсорбционного сдвига потенциала. По уравнению (46а) была найдена адсорбция ионов брома на платиновом, родиевом и иридиевом электродах в 10"2 н. НВг + 1 н. H2S04 [79]. Сопоставление рассчитанных величин Г4 с полученными прямыми аналитическими методами (по изменению концентрации ионов брома в растворе) также служит подтверждением правильности термодинамической теории обратимого электрода. В рассматриваемых системах, благодаря избытку фонового электролита, DIl — RT
= — у D In Ch а поэтому уравнения (45)—(48) можно переписать,
RT
Заменяя dp,- на — у D In Ch а условие pt — = const—на сг = const.
Если при изменении концентрации специфически адсорбирующихся ионов происходит изменение не только их химического потенциала, но и химического потенциала ионов противоположного знака, то в таком случае оказываются справедливыми следующие соотношения [39, 40]:
/ DQ‘ / Аг.
V ^са /1н+. ег ~ ^ дег /ин+. иса ^ дег пса (49) (дЕг /ДГ. 5
Wca^’^HH— W /ДН+. ^СА V иСА
Уравнение (41) можно привести к виду:
(1ЁлЛ = -(^А (51)
Wh+Л’. пса ^ ‘ Пн+> пСА V № /пн+- пСА
Таким образом, измерение величин (dEr/dicp)Q>t (Afi+ и (DER/diH+)Q‘, ЦСа позволяет по уравнениям (50) и (51) определить зависимость величин Г+ и Г_ от потенциала, т. е. провести раздельное определение адсорбции аниона и катиона. Справедливость этого вывода была подтверждена в работе [80].
Для проверки теории были использованы данные по совместной адсорбции ионов на платине. При совместной адсорбции ионов 1 и 2 при постоянном потенциале электрода в присутствии большого избытка постороннего электролита уравнение Гиббса приводится к виду:
Da = —Гх dux — Г 2 (52)
Отсюда следует
(ЛЧ/ащ)^ = (ar2/dp1)(it (53)
/ — 10-» н. H2S04 + 2- 10-s н, Cs2S04 + х н. Na2S04; 2 — 10"» н H2S04 + 2« 10-а н. NajS04 + х н. Cs2S04.
Таким образом, наклоны изотерм вытеснения данного иона другим с поверхности электрода при постоянном потенциале должны совпадать. В этом случае также ввиду наличия избытка
RT
Посторонней соли вместо <ipt — можно использовать — р — 4 In ct-.
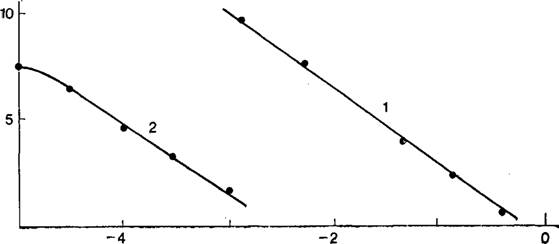
На рис. 2 сопоставлены зависимости адсорбции ионов цезия от концентрации ионов натрия и адсорбции ионов натрия от концентрации ионов цезия. Кривые этих зависимостей, действительно, оказываются параллельными [81 ]. Аналогичное явление отмечено при совместной адсорбции сульфат — и хлорид — анионов в кислых растворах и бромид — и иодид-анионов в щелочных растворах на платинированной платине [82] Совпадение наклонов изотерм вытеснения можно рассматривать как подтверждение справедливости термодинамической — теории обратимого электрода.
|
Рис. 2. Изотермы вытеснения катионов цезия катионами натрия (1) и катионов натрия катионами цезия (2) при Ег = 0 на платинированном платиновом электроде в растворах: |
|
Lg[Na2S04]; lg[Cs2SOj (г-экв/л) |
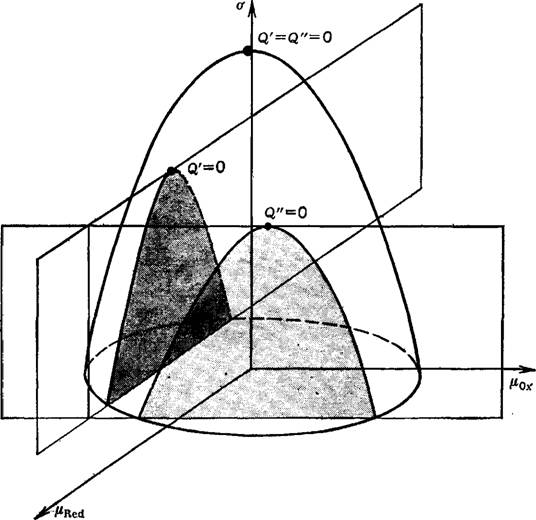
Для электрода, на котором протекает процесс (15), обратимая поверхностная работа в растворе с постоянной концентрацией фонового электролита является функцией р0х и M-Red и в координатах <т, р0х, pRed может быть представлена поверхностью параболоида. Сечение этого параболоида плоскостью Pox = const дает электрокапиллярную кривую 1-го рода, а сечение плоскостью pRed = const — электрокапиллярную
|
Рис. 3. Электрокапиллярные кривые 1-го и 2-го рода обратимого электрода, представленные в виде сечений поверхности а плоскостями [X0X=Const и Fx^Ed— Const [64]. |
Кривую 2-го рода. Максимум параболоида отвечает условию
= Q" = о (рис. 3) [64].
На металлах группы платины а оказывается функцией рн+ и Рн- Электрокапиллярные кривые 1-го и 2-го рода есть не что иное, как сечение поверхности параболоида плоскостями рн+ = = const или рн = const. Электрокапиллярные кривые платинового электрода (с точностью до константы интегрирования), полученные путем интегрирования уравнений (31) и (32), показаны на рис. 4 [2]. Эти кривые по форме напоминают электрокапиллярные кривые ртутного электрода, но свидетельствуют о существенно большей, чем на ртути, зависимости а от потенциала. Это связано с тем, что на платине на величину а влияет
|
Рис. 4. Электрокапиллярные кривые 1-го (1—3) и -2-го (4—И) рода для платинированного платинового электрода в 0,1 н. КС1 при рН 2,3 (/); 7,0 (2); 12,0(3) и при Еп В 0,1 (4); 0,15 (5); 0,2 (6); 0,3 (7); 0,4 (8); 0,5 (9); 0,6 (10); 0,7 (11). |
Не только адсорбция ионов раствора, но и адсорбция атомов водорода и кислорода. Другая существенная особенность кривых 1-го рода состоит в зависимости потенциала электрокапиллярного максимума от рН раствора, что в соответствии с уравнением электрокапиллярности вызвано влиянием рН на адсорбцию водорода и кислорода. В [2, 54, 56] приведены и обсуждены термодинамические соотношения, описывающие влияние рН на потенциалы нулевого полного заряда металлов группы платины.
На основе уравнения (33) были выведены соотношения для зависимости адсорбции водорода и кислорода от рН раствора и концентрации электролита [36, 47, 83].
В работе [84] теория электрокапиллярности была распространена на явления обратимой адсорбции органических веществ на металлах, адсорбирующих водород и кислород. В предположении постоянства рН раствора и концентрации электролита и при условии, что изменение концентрации органического вещества не влияет на химические потенциалы других компонентов системы, можно записать
Do = —Q’ DEr — Г org dnorg (54)
Откуда следует, в частности
(di0rg/dEr) Rorg = — (dQ‘/dTorg)Er (55)
Или
(Д AGorgldEr)Torg = — (dQ’/ДTorg)Er (56)
Где AG0rg — стандартная свободная энергия адсорбции органического вещества.
Анализ соотношения (56) приводит к выводу, что на электродах, обратимо адсорбирующих водород, кислород и органическое вещество, максимум T0Rg должен приходиться на интервал потенциалов, в котором адсорбция водорода и кислорода минимальна [84]. К сожалению, пока не удалось подвергнуть этот вывод экспериментальной проверке, так как не было найдено органическое вещество, которое бы обратимо адсорбировалось на металлах группы платины.
В работах Фрумкина и сотрудников [72—74 ] было детально исследовано электрокапиллярное поведение системы Hg, Tl, Т1+, Н20. Границу раздела в этом случае удобнее всего определить условием rHg = 0. Если концентрации солей Т1А и СА в растворе достаточно малы так, что можно принять рн*о = = const, то эту систему можно, трактовать аналогично платино — водородному электроду и записать:
Do=— rT, dpT1 — rT1AdpT1A— ГСА DpCA (57)
Из уравнения (57) следует
(Aa/AЈ—VT1A. ПСА= = ГТ1 = ЛТ1 (58)
(до/дЕ.)^ = Q" = ГТ1+ = — е — ЛТ)+ (59)
Где Лт1 — количество Т1, присутствующее в поверхностном слое в виде атомов;
Лп+ — величина адсорбции ионов Т1+, остающихся в ионной обкладке двойного слоя.
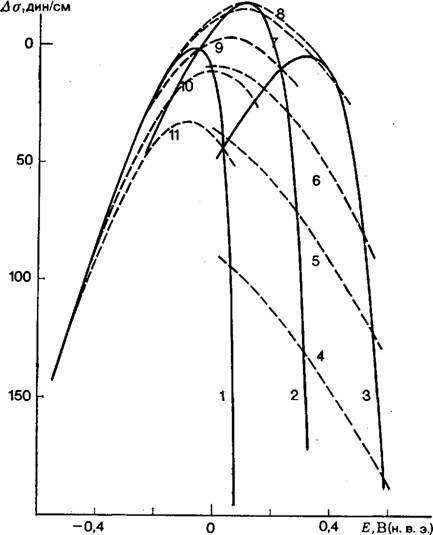
Концентрация Т1+ (х) в растворах х М TlN03 + (1 — х) М KN03: 1 — 0,001; 2 — 0,005; 3 — 0,01; 4 — 0,05; 5 — 0,1. Концентрация T1 в амальгамах: 6 — 0,002; 7 — 0,014; 8 — 0,12; 9 — 0,7; 10 — 4,9; 11 — 7,8% (ат.).
Электрод сравнения: 9,9%-ная амальгама TI в 0,1 М TlN03 + + 0,9 М KN03.
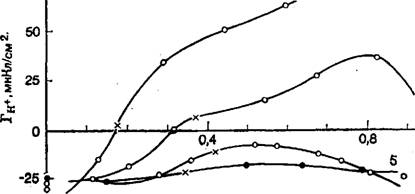
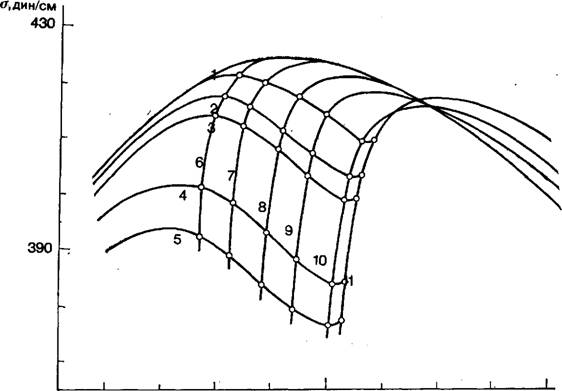
В [74] приведены семейства электрокапиллярных кривых 1-го и 2-го рода для системы Hg, TI, ТГ, Н20 и показано, в каких условиях величинами V4Ti или V4Ti+ можно пренебречь и в каких условиях это допущение неприменимо. Часть полученных кривых воспроизведена на рис. 5.
|
Рис. 5. Электрокапиллярные кривые 1-го и 2-го рода в системе Hg, Т1, ТГ, Н20 [73]. |
|
0,4 0 -0,4 Ё, В |
Исходя из представлений о полном и свободном зарядах, в [49, 50 ] была рассмотрена электрокапиллярная зависимость, получающаяся при выполнении условия
[Ох] + у [Red] = ConsT (60)
Где у — постоянная величина.
При у = (DRed/Dox,)1/2> гДе DRed и D0x — коэффициенты диффузии ред — и окс-форм, уравнение (60) соответствует изменению концентрации Ох и Red у поверхности электрода в полярографических условиях. Обобщенное понятие о заряде электрода позволяет более последовательно трактовать электрокапиллярные кривые в редокс-системах, чем это было сделано в [85—87], и истолковать полярографические ‘«электрокапиллярные кривые», а также электрокапиллярные кривые для неорганических и органических редокс-систем, получаемые с помощью капиллярного электрометра [49, 50, 88].
 2 января, 2013
2 января, 2013  admin
admin 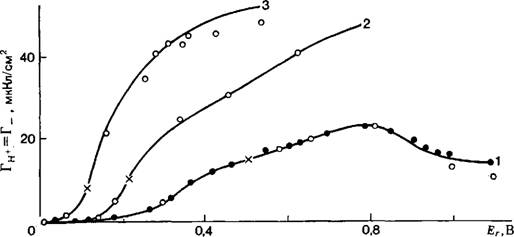
 Опубликовано в рубрике
Опубликовано в рубрике 