Уравнения (24) и (25) являются общими для любой плоской межфазной области между двумя несжимаемыми ньютоновскими жидкостями, если только к описанию локальных свойств применимо условие аксиальной симметрии. В частности, они тогда должны быть справедливыми для любимой модели, используемой специалистами по макроскопической динамике жидкости, а именно: бесконечно тонкая межфазная поверхность. В такой поверхности локальные свойства меняются скачком при пересечении плоскости 2 = 0. Запишем в явном виде:
Ц = и" = и’ = 4" + и11) + 4- * W (ип — и[2])
О 1 (ду1х дК1 1 (dVx Wl Г
Х N ‘ о
О
О
Здесь h (z) — функция Хэвисайда: h (z) = —1 для z < 0 и h (z) = 1 для z > 0. Из уравнений (26), а также рис. 3 следует, что в этой модели межфазной поверхности плотность, коэффициенты вязкости и статический тензор давлений разрывны. Составляющие вектора скорости непрерывны, но производные от тангенциальных составляющих dVJdz и ‘ dVJdz Разрывны, в то время как для нормальной составляющей разрывна вторая производная d2VJdz2. Наконец, величина 0° есть скорость дилатации поверхности разрыва
|
< Дх |
|
К Ду |
|
00 = |
|
= vs-v° |
И условие несжимаемости (9) выполнено.
Подстановкой уравнений (26) в (24) и (25) все интегрирования для такой модели межфазной поверхности могут быть формально закончены (интересующийся читатель может проследить за одним из этих интегрирований в Приложении II, Но нас не интересуют явные результаты). Для наших целей достаточно допущения, что все эти интегралы имеют поря-
Док 0 (Az) или меньше, т. е. они являются произведениями таких величин объемных фаз, как р1, р11 и т. д., на интервал Az. Наша цель при построении модели межфазной поверхности состояла в сравнении положения этой модели с реальной межфазной поверхностью. Этого мы достигаем, прибавляя и вычитая результаты для модельных интегралов к уравнениям (24) и (25).
В качестве примера одной из этих операций рассмотрим интеграл j Ptdz, который появляется в уравнениях (25). Запишем
|
Dz-f— +I [~Т(pI + рП) + ~Тh (z) (рП ~ pl)] ^ = — V + о (Дz) У = J [4 + рП) + 4" Л (Z) {PU ~ Pl) — Pt Dz |
IЛ л = | [Л — 4" ^ + PU)—Т h <г) {рП — р1)
Где
(27)
Является, очевидно, избыточной капиллярной величиной, тесно связанной с поверхностным натяжением, определенным уравнением Баккера (5) для статической межфазной поверхности.
В действительности я использовал для обеих величин одно и то же обозначение у, но вопрос о согласованности уравнений (5) и (27) рассмотрю в следующем разделе.
Аналогичным образом можно привести интегралы j рVxdz И j р‘Vxdz к следующим:
J 9Vx Dz = J — V® [ — j — (p1 + p11) + ~R h & (p" ~ рг) ] } dz + 0
(28)
+ 0(Az) (29)
Дальнейшие упрощения я обосновываю доводами, что поле скорости в экспериментальной системе очень слабо меняется на толщине Az рассматриваемой нами межфазной поверхности. Конечно, производные dVJdz и DVy!Dz значительно меняются на этом расстоянии, но я тем не менее предполагаю, что толщина Az может — быть выбрана столь малой, что в хорошем при-
Ближении V V1 ^ Vй везде внутри межфазной области. Если бы это было не так, экспериментатор наблюдал бы столь большие изменения в поле скорости по обе стороны межфазной поверхности, что был бы вынужден допустить существование
|
|
А б
Рис. 4. Сравнение диффузной экспериментальной межфаз ной поверхности с моделями, приведенными на рис. с
А — плотность р монотонно меняется в анизотропной облает» избыточная капиллярная плотность массы Г, определенна уравнением (30), является суммой заштрихованных площаде} подходящим выбором разделяющей поверхности г = О, можн обратить Г в нуль;
Б — сдвиговая вязкость изображена с резко выраженным мак симумом: поверхностная сдвиговая вязкость ц’, определенна уравнением (31), равна заштрихованной площади; для приведер ной разделяющей поверхности 2=0, вязкость г) положительш но т| может быть сделана равной нулю достаточно большим см( щением плоскости г — 0 вправо.
В его системе плоскости скольжения, совпадающей с оптиче ски наблюдаемой межфазной поверхностью. Эксперименталь ных свидетельств о существовании такой плоскости сколь жения нет; поэтому-то я и выбираю величину в уравнения: (28) и (29), являющуюся ^-составляющей вектора скорост] межфазной поверхности, и полагаю Vx = Vx во всей облает] интегрирования. Вынося V°x из-под знака интеграла, получае1 из уравнений (28) и (29)
J‘PVxdz= rvj-f 0(Az);
J‘ n‘Vxdz = r)V°x-t-0(Az)
Где
Г = J [р———- g — (р1 + р11)——— LTh(z) (р11 — р1)] dz (30)
|
Dz (31) |
11=1 К -4- W+4л (2) ^ — ^
Избыточные капиллярные плотность массы и сдвиговая вязкость.
Уравнения (30) и (31) — основные в том классе явлений капиллярной реологии, рассмотрение которых является целью этой статьи. Возможные формы подынтегральных выражений изображены на рис. 4. Без помощи строгого статистико-механи — ческого рассмотрения установить аналитический вид подынтегральных выражений невозможно, но выбранная форма, по крайней мере, согласуется с известными из опыта свойствами реальных жидкостей. Мы вернемся к этому вопросу в следующем разделе. Сейчас же достаточно отождествить интегралы (30) и (31) с заштрихованной площадью на рис. 4. Очевидно также, что значения этих интегралов зависят от положения разделяющей поверхности Z — 0, которая в нашей модели является поверхностью разрыва функции Хэвисайда H (Z).
Последовательное приложение этих методов к уравнениям баланса импульса (24) и (25) позволяет привести их к виду:
Нормальная составляющая —
П
О = | Ргг + 0 (AZ) (32)
I
Тангёнциальные составляющие —
4г = | + "Ж+ * IF + IVK + 0 (А.)
(33)
II
— TV0 = Dt VY
I
Где у, Г и г] определены уравнениями (27), (30) и (31), а
* = ] И- —I — Л (г) (fx11 — f^1)] ^ (34)
Избыточная капиллярная дилатационная вязкость.
Наряду с у, Г и ц величина K не определена точно, пока не сделан выбор положения разделяющей поверхности Z = 0.
 29 декабря, 2012
29 декабря, 2012  admin
admin 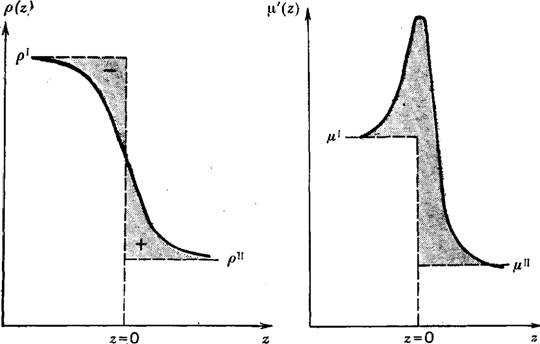
 Опубликовано в рубрике
Опубликовано в рубрике 