Про теорию капиллярности Гиббса можно сказать, что она очень проста и очень сложна. Проста потому, что Гиббсу удалось найти метод, позволяющий получить наиболее компактные и изящные термодинамические соотношения, в равной мере применимые к плоским и искривленным поверхностям. «Одной из основных задач теоретического исследования в любой области знания, — писал Гиббс, — является установление такой точки зрения, с которой объект исследования проявляется с наибольшей простотой» [2]. Такая точка зрения в теории капиллярности Гиббса — это представление о разделяющих поверхностях. Использование наглядного геометрического образа разделяющей поверхности и введение избыточных величин позволило максимально просто описать свойства поверхностей и обойти вопрос о структуре и толщине поверхностного слоя, который во времена Гиббса был совершенно не изучен и до сих пор остается решенным, далеко не полностью. Избыточные величины Гиббса (адсорбция и другие) зависят от положения разделяющей поверхности, и последнее может быть также найдено из соображений максимальной простоты и удобства.
Гиббс использовал два основных положения разделяющей поверхности: такое, при котором адсорбция одного из компонентов равна нулю (сейчас эту поверхность называют эквимолекулярной), и положение, для которого исчезает явная зависимость поверхностной энергии от кривизны поверхности (это положение было названо Гиббсом поверхностью натяжения). Эквимолекулярной поверхностью Гиббс пользовался для рассмотрения плоских жидких поверхностей (и поверхностей твердых тел), а поверхностью натяжения — для рассмотрения искривленных поверхностей. Для обоих положений сокращается число переменных и достигается максимальная математическая простота.
Теперь о сложности теории Гиббса. Будучи очень простой в математическом отношении, она все же трудна для восприятия; происходит это по нескольким причинам. Во-первых, теорию капиллярности Гиббса невозможно понять в отрыве от всей гиббсовской термодинамики, в основе которой лежит весьма общий, дедуктивный метод. Большая общность теории всегда придает ей некоторую абстрактность, что, конечно, отражается на легкости восприятия. Во-вторых, сама теория капиллярности Гиббса есть обширная, но условная система, требующая единства восприятия без отвлечения от отдельных ее положений. Дилетантский подход к изучению Гиббса просто невозможен. Наконец, немаловажным обстоятельством является то, что вся упомянутая работа Гиббса написана весьма конспективно и очень трудным языком. Эта работа, по словам Рэлея, «слишком сжата и трудна не только для большинства, но, можно сказать, для всех читателей» [3]. По мнению Гуген- гейма, «гораздо легче использовать формулы Гиббса, чем понимать их» [4].
Естественно, что использование формул Гиббса без их истинного понимания приводило к появлению многочисленных ошибок в интерпретации и применении отдельных положений теории капиллярности Гиббса. Много ошибок было связано с непониманием необходимости однозначного определения положения разделяющей поверхности для получения правильного физического результата. Ошибки такого рода часто встречались при анализе зависимости поверхностного натяжения от кривизны поверхности; не избежал их даже один из ‘«столпов» теории капиллярности — Баккер. Пример ошибок другого рода — неправильная интерпретация химических потенциалов при рассмотрении поверхностных явлений и внешних полей.
Уже вскоре после опубликования теории капиллярности Гиббса высказывались пожелания о ее более полном и подробном пояснении в научной литературе. В цитированном выше письме к Гиббсу Рэлей предлагал, чтобы эту работу взял на себя сам Гиббс. Однако выполнено это было значительно позже: Райе подготовил комментарий ко всей теории Гиббса [5 стр. 505—708], а отдельные ее положения комментировались в трудах Фрумкина, Дефея, Ребиндера, Гуггенгейма, Тол — мена, Баффа, Семенченко и других исследователей. Многие положения теории Гиббса прояснились, и для их обоснования были найдены более простые и эффективные логические приемы.
Типичным примером является эффектная работа Кондо [6], в которой был предложен наглядный и простой для понимания метод введения поверхности натяжения путем мысленного перемещения разделяющей поверхности. Если мы напишем выражение для энергии равновесной двухфазной системы а—р (а — внутренняя и fi — наружная фазы) со сферической поверхностью разрыва
U = TS — paVa — + + № (1)
I
И будем мысленно менять положение разделяющей поверхности, т. е. менять ее радиус г, то, очевидно, такие физические характеристики, как энергия U, температура Т, энтропия 5, давление Р, химический потенциал ^го компонента fx, и его масса ть а также полный объем системы Va + Va при этом не
Изменяется. Что же касается объема Va = -у — лг3, площади
Л = 4яг2 и поверхностного натяжения а, то эти величины будут зависеть от положения разделяющей поверхности и потому для указанного мысленного процесса изменения г мы получаем из (1)
—PadVa-{-P&dVp-{-odA + Ada = 0 (2)
Или
Уравнение (3) определяет нефизическую (это обстоятельство отмечено звездочкой) зависимость поверхностного натяжения от положения разделяющей поверхности. Эта зависимость характеризуется единственным минимумом а, который и соответствует поверхности натяжения. Таким образом, по Кондо, поверхность натяжения—эта такая разделяющая поверхность, для которой поверхностное натяжение имеет минимальное значение.
Как известно, Гиббс вводил поверхность натяжения иным путем. Он исходил из основного уравнения теории капиллярности
СШ = TdS + о dA — f J" dml — f Сг dcx + СгАсг (4)
I
(черта сверху означает избыток для произвольной разделяющей поверхности с главными кривизнами С, и С2) и рассматривал физический (а не чисто мысленный) процесс искривления поверхности при заданном ее положении и фиксированных внешних условиях.
По Гиббсу, поверхности натяжения соответствует такое положение разделяющей поверхности, при котором искривление поверхностного слоя при постоянстве внешних параметров не — сказывается на поверхностной энергии и соответствует также условию:
До/дг = О (5)
Гуггенгейм так комментирует доказательство Гиббса: «Я нашел рассмотрение Гиббса трудным, и чем тщательнее я изучал его, тем более неясным оно мне казалось» [4]. Это признание свидетельствует о том, что понимание поверхности натяжения по Гиббсу встречало трудности даже у специалистов в области термодинамики.
Что касается подхода Кондо, то он понятен с первого взгляда. Однако необходимо убедиться, что поверхности натяжения по Гиббсу и Кондо адекватны. Это можно продемонстри-
Ровать, например, используя гидростатическое определение поверхностного натяжения [7, стр. 61]
Г ЯР
|
1 О = —т- |
|
(6) |
J (p*-Pt) /2dr‘ + J (F»-Pt) г’Чг’
RA
Где Pt — локальное значение тангенциальной составляющей тензора давления; Г‘ — радиальная координата; радиусы Ra и R& ограничивают поверхностный слой.
Дифференцирование (6) при мысленном перемещении разделяющей поверхности и постоянстве физического состояния (подход Кондо) приводит к уравнению (3). Дифференцировав ние же при искривлении поверхностного слоя и постоянстве физического состояния (подход Гиббса, в этом случае Ra и R& Переменны) дает
+ (7,
Где учтено, что Pt (Ra) = Ра и Pt (Rt) = PP.
Из уравнений (7) и (3) видно, что условие (5) эквивалентно условию (do/dr)* = 0 и, следовательно, более простой и наглядный подход Кондо адекватен подходу Гиббса.
В качестве другого примера рассмотрим теорию упругости жидких пленок, сформулированную впервые Гиббсом в рамках его теории капиллярности. Ныне этот вид упругости называют гиббсовской упругостью (см. обзор [8]). Она характерна для пленок растворов поверхностно-активных веществ.
В рассуждениях Гиббса можно выделить общее обоснование жидких пленок и вывод термодинамической формулы для модуля упругости частично открытой пленки. Общее обоснование было дано Гиббсом в словесной форме [1]: «Если пленка имеет два или более компонентов, потенциалы которых не поддерживаются постоянными под влиянием смежных газовых масс, то они, вообще говоря, не будут находиться в том же отношении внутри пленки, что и на ее поверхностях, но те компоненты, которые уменьшают натяжение, будут находиться на поверхностях в большем соотношении. Если пленка растянута, то этих веществ не будет достаточно для поддержания той же объемной и поверхностной плотности, как раньше, и этот недостаток вызовет некоторое увеличение натяжения». В этой фразе правильно вскрывается механизм возникновения упругости пленок растворов поверхностно-активных веществ.
Где Е — модуль упругости пленки;
Г2(1)—относительная адсорбция второго компонента; щ — его химический потенциал;
Gt — — количество 1-го компонента на единицу площади
Пленки.
Как отмечалось в литературе [8, 9], вывод этой формулы Гиббсом весьма противоречив. Одна из возможных причин этого состоит в том, что Гиббс пользовался представлениями разработанной им термодинамики открытых систем, тогда как рассматриваемый случай относится к закрытым или частично закрытым системам. В результате формула (8) Гиббса не нашла практического применения и возникла необходимость переформулирования теории гиббсовской упругости пленок [9, 10; 11 стр. 254; 12—14]. Точная формула для модуля гиббсовской упругости я-компонентной пленки имеет вид [8, 14]
|
|
Где с,- и fi — концентрация и коэффициент активности i—Го компонента;
H — толщина пленки, определяемая как расстояние между разделяющими поверхностями пленки, для которых адсорбция я-го компонента (растворителя) равна нулю.
Формула (9) удобна для практического использования, так как явно содержит толщину пленки, и все величины, входящие в (9), могут быть определены из опыта.
Приведенные примеры показывают, что путь понимания теории капиллярности Гиббса был долгим и продолжается в наше время. Многие работы посвящены различным способам вывода уравнения адсорбции Гиббса, интерпретации гиббсов — ских величин для твердых тел и другим вопросам теории капиллярности Гиббса.
 27 декабря, 2012
27 декабря, 2012  admin
admin 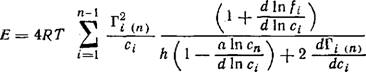
 Опубликовано в рубрике
Опубликовано в рубрике 