|
Рис. 9 |
Капиллярные волны — это другое название известного всем явления «ряби» на поверхности жидкости. Образуются эти волны под влиянием небольших возмущений и их возникновение связано с силами поверхностного натяжения. Механизм образования капиллярных волн в общих чертах следующий. Под действием тех или иных внешних воздействий поверхность жидкости в данном месте «вдавливается», становясь вогнутой (рис.9, а), Давление на слои жидкости под этой вогнутой поверхностью становится меньше (на величину ![]() ), чем давление в соседних слоях, где поверхность осталась плоской. Возникшая таким образом разность давлений заставляет жидкость из соседних слоев приливать под вогнутую поверхность, и жидкость снова поднимается к начальному уровню, но проходит его по инерции за счет накопленной кинетической энергии. Поверхность поэтому станет выпуклой, и давление, обусловленное кривизной ее поверхности, будет теперь направлено вниз (рис. 9, б).
), чем давление в соседних слоях, где поверхность осталась плоской. Возникшая таким образом разность давлений заставляет жидкость из соседних слоев приливать под вогнутую поверхность, и жидкость снова поднимается к начальному уровню, но проходит его по инерции за счет накопленной кинетической энергии. Поверхность поэтому станет выпуклой, и давление, обусловленное кривизной ее поверхности, будет теперь направлено вниз (рис. 9, б).
Ясно, что такого рода колебания жидкости в одном месте заставит и соседние точки совершать такие же колебания. Это и значит — что явление имеет волновой характер. Капиллярные волны отличаются малой амплитудой и малой длиной волны. Из-за малости амплитуды можно пренебречь влиянием силы тяжести, которая может вызывать такое же действие (силе тяжести обязаны и происхождением крутые морские волны). Волны только в тех случаях и называются капиллярными, когда в их образовании участвуют только силы поверхностного натяжения и они образуются за счет значительной кривизны на гребне и впадине волны.
Расчет показывает, что параметры капиллярных волн связаны с коэффициентом поверхностного натяжения следующим уравнением:
|
(6) |
![]()
Где N — частота колебаний в волне, ![]() — длина волны и
— длина волны и ![]() — плотность жидкости. Формула (6) и может быть использована для определения коэффициента поверхностного натяжения жидкости, плотность которой известна. Для этого необходимо измерить частоту колебаний и длину волны. Обычно измеряют скорость распространения волн, с которой частота колебаний связана простым соотношением.
— плотность жидкости. Формула (6) и может быть использована для определения коэффициента поверхностного натяжения жидкости, плотность которой известна. Для этого необходимо измерить частоту колебаний и длину волны. Обычно измеряют скорость распространения волн, с которой частота колебаний связана простым соотношением.
 19 декабря, 2012
19 декабря, 2012  admin
admin 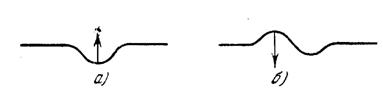
 Опубликовано в рубрике
Опубликовано в рубрике 