Лако-красочные материалы — производство

Итоговая энергия взаимодействия представляет собой основу для изучения адге­зии и полимерных материалов. Давайте представим себе ситуцию, при которой два атома или две молекулы находятся в непосредственной близости друг к другу. Для инертных газов или молекул, например, метана, характерно сферическое симме­тричное распределение заряда. В этом случае можно предположить, что благодаря отсутствию заряда или действительного разделения заряда между рассматриваемы­ми двумя типами частиц не должно существовать никакого взаимодействия. Одна­ко в данном случае может быть замерено ярко выраженное взаимодействие и его обнаруживают при анализе любых материалов. Описание источника этого взаимо­действия основывается естественно на анализе взаимодействия между постоянным диполем и наведенным диполем. При сферическом симметричном распределении зарядов существует вероятность того, что в какой-то любой мгновенный момент времени всеэлсетгроны в атоме или молекуле оказываются на одной или другой сто-

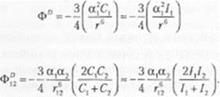ронс атома или молекулы. Если это происходит, атом или молекула имеют частич­но неэкраиированные ядра или ядро на одной стороне и избыток электрического заряда на другой стороне. В этом случае появляется мгновенный диполь, который может индуцировать мгновенный диполь в других атоме или молекуле, имеющих с<|>еричсское распределение зарядов. В результате этою появляется полезная потен­циальная энергия взаимодействия, которая приводит к возникновению взаимодей­ствия между этими двумя атомами или молекулами. Так как такие взаимодействия являются мгновенными, можно предположить, что их величина должна быть незна­чительной. Уравнение, которое описывает потенциальную энергию взаимодействия между двумя атомами или молекулами, определяемую взаимодействием между мгновенный диполем и мгновенным наведенным диполем, имеет вид

Первое выражение справедливо для одинаковых атомов или молекул, в то время как второе выражение относится к неодинаковым атомам или молекулам. В при­веденных выше уравнениях параметры а представляют приведенные выше значе­ния поляризуемости, С молекулярные константы, которые могут быть аппрок­симированы параметром /, представляющим собой ионизационный потенциал для атома или молекулы і. Рассматриваемая потенциальная энергия взаимодействия представлена символом Ф°, где D обозначает взаимодействие под действием дис­персионных сил. Термин дисперсионная сила принят, исходя из аналогичной связи этой силы с дисперсией света в видимой и ультрафиолетовой областях спектра. По существу, «дисперсионная сила» не является точным описанием данного явления и может вводить в некоторое заблуждение. Однако в специальной литературе этот термин принят для описания силы взаимодействия между мгновенным диполем II наведенным диполем.

При анализе уравнений потенциальной энергии дисперсионных сил можно от­метить три момента. Во-первых, взаимодействие прямо связан») с поляризуемостью каждого из взаимодействующих типов частиц. Следовательно, для атомов или моле­кул, которые имеют свободно связанные электроны (свободно связанные электроны более легко перемещаются в электрическом поле), характерно более сильное взаи­модействие дисперсионных сил, чем для молекул, имеющих компактно удерживае­мые электроны. Во-вторых, взаимодействие дисперсионных сил зависит от первого ионизационного потенциала, присущего частицам. В-третьих, взаимодействие дис­персионных сил обратно пропорционально шестой степени расстояния, разделяю­щего две частицы. Взаимодействующие частицы должны быть расположены близко друг к другу для того, чтобы потенциальная энергия взаимодействия имела какое — либо принципиальное значение. В данном случае необходимо привести сравнение с потенциальной энергией Кулоновского взаимодействия, которая зависит от об­
ратной величины расстояния между частицами. При взаимодействии заряд-заряд влияние силы распространяется на очень большие расстояния.

Более подробное описание взаимодействия дисперсионных сил между поверх­ностями основано на законах квантовой электродинамики, которые не рассматри — вакггся в данной книге. Наиболее часто для объяснения этих эффектов используют теорию Л ифшица [б). Однако теория Лифшица довольно трудна для понимания и в данном случае предпочитают использовать более простое объяснение, предложен­ное Гримли |6]. Израелашвили [7] щіедложил методологический подход к аппрок­симации результатов измерений, необходимых для вычисления взаимодействия ДИСПС|К’И01П1ЫХ сил между двумя телами.